你好,我是王健伟。
聊过了二叉树的遍历问题,终于要开始写程序了,所以今天就来聊聊存储二叉树的几种方法。
二叉树的存储一般有两种方式,一种是基于数组的顺序存储方式,一种是链式存储方式。它们有什么不同呢?
顺序存储方式
顺序存储方式是用一段连续的内存单元(数组)依次从上到下、从左到右存储二叉树各个节点元素。
假设我们存储的是一棵完全二叉树,如果把根节点存储在数组中下标i = 1的位置,那么根据之前讲解的二叉树编号规律[(二叉树性质6)],左子节点就存储在下标2 * i = 2的位置,右子节点就存储在2 * i + 1 = 3的位置。这样就可以通过下标把整棵树串起来。
因为节点编号从1开始,所以数组中下标为0的位置可以空出来不用,让数组下标和节点编号保持一致。虽然这样浪费了一个存储空间,不过这点你可以自由决定。
参考下图1。
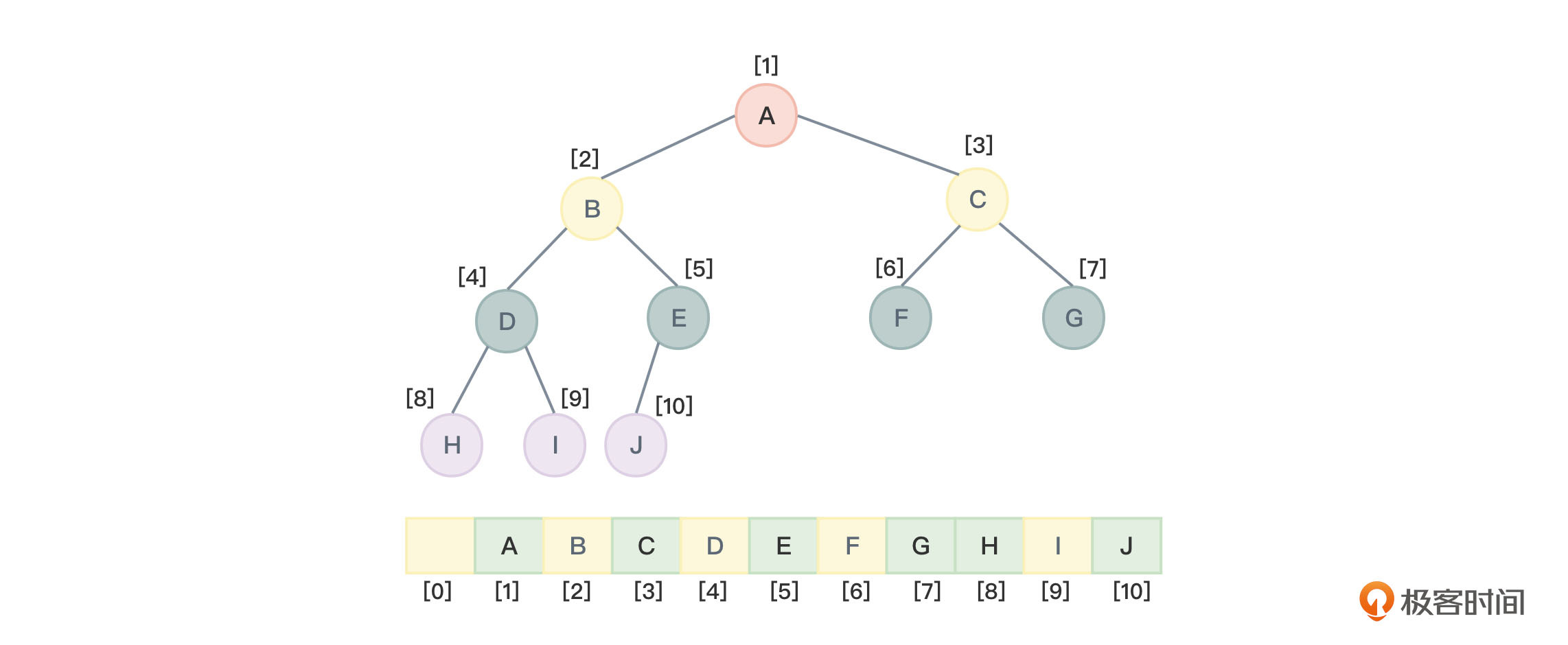
不难看到,数组的下标可以体现出节点的存储位置。换句话说,数组的下标能够体现出节点之间的逻辑关系(父子、兄弟)。
但如果存储的不是一棵完全二叉树,而是普通二叉树,那么存储的时候,也需要将其按照完全二叉树的方式来编号存储,这样肯定会浪费较多的数组存储空间。
参考下图2。
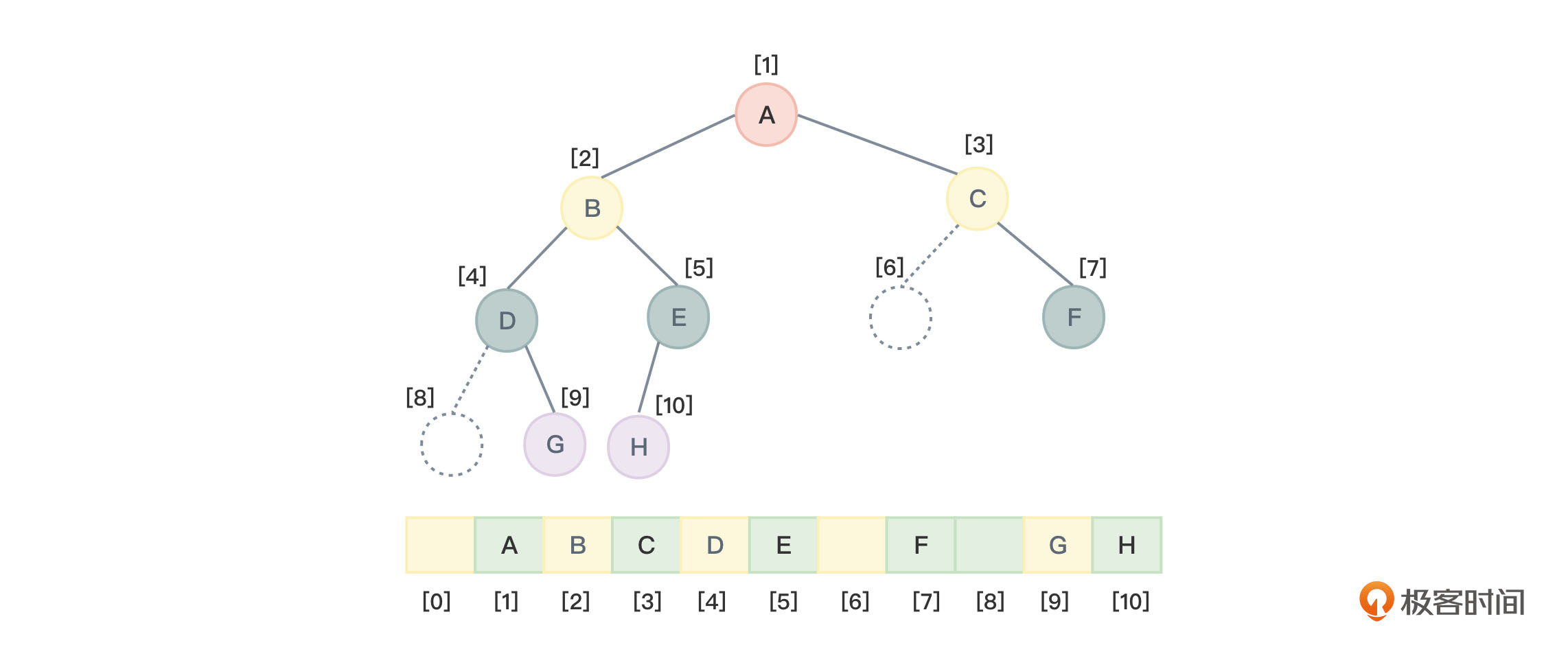
图2中虚线表示的节点表示不存在的节点,但在存储时却要给其留出位置。可以看到,下标6、8的数组空间都被浪费掉了。
你可以想一种极端的情况:如果有一棵深度为4的右斜树需要保存,会浪费多少个数组空间呢?
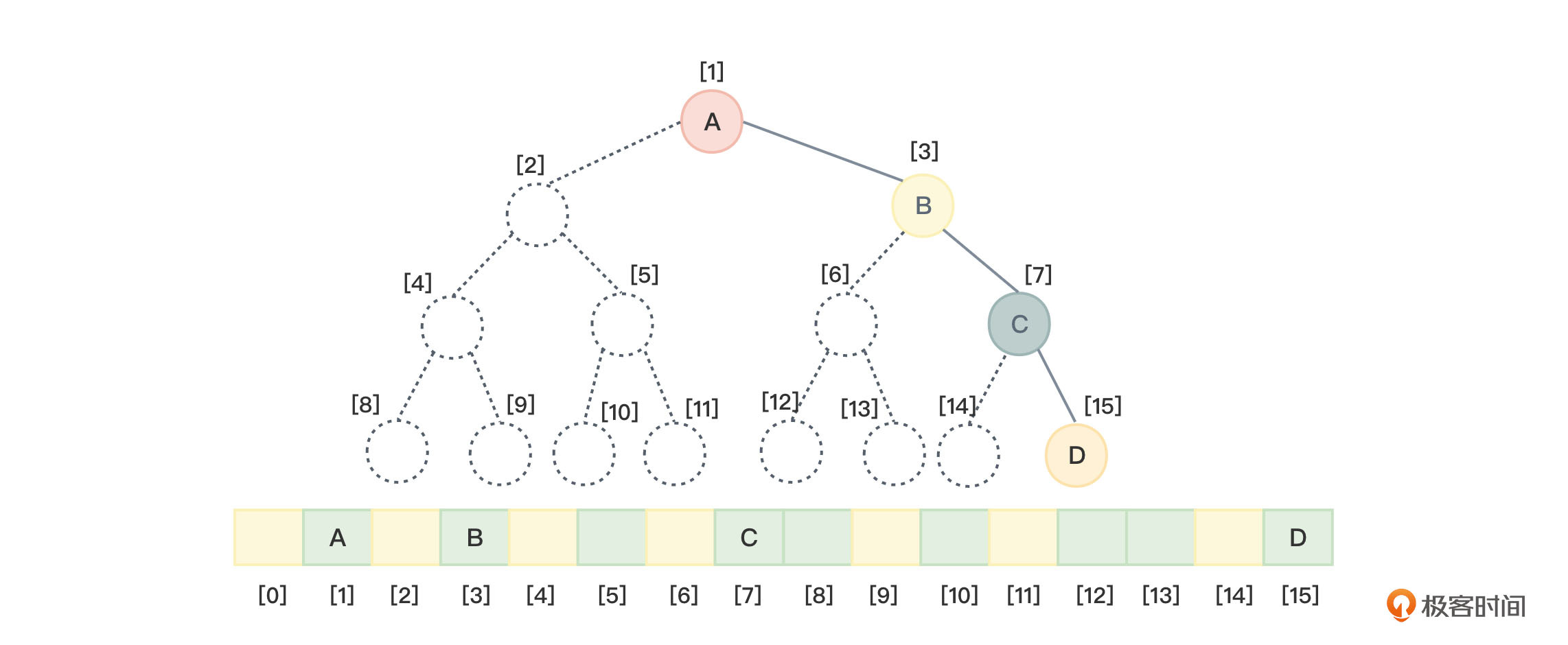
根据二叉树性质2,“高度为k的二叉树至多有$2^{k}$-1个节点”,存储高度为4的二叉树,最坏情况下空间需求是$2^{4}$-1=15,因为下标为0的空间不使用,所以最坏情况下空间需求是$2^{4}$=16,而图3的右斜树恰恰需要$2^{4}$=16个存储空间。即便下标为0的位置不计算在内,也整整浪费了11个位置。
可是,完全二叉树就不会存在这个问题。这就是完全二叉树最后一层叶节点都靠左侧排列这种硬性规定所带来的存储益处。换句话说,顺序存储结构一般是用于存储完全二叉树。
链式存储方式
链式存储方式要存储额外的左右子节点的指针,而顺序存储方式是不需要指针的,所以通常来讲,链式存储方式多用于存储普通的二叉树。
链式存储中,二叉树的每个节点最多有两个子节点,所以为每个节点设计结构时一般都包括一个数据域和两个指针域,分别指向左孩子节点和右孩子节点。至于没有用到的指针,设置为nullptr即可。结构示意图如图4所示:
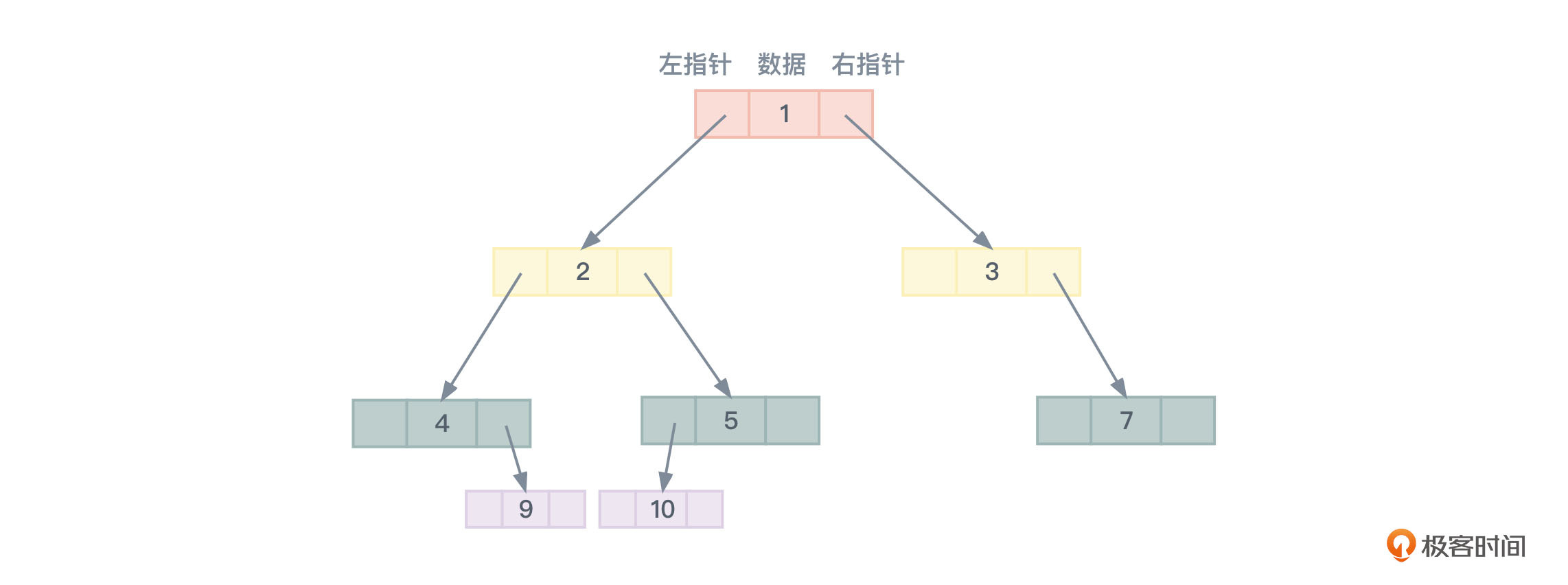
从图4可以看到,只要拎住最上面的根节点,就可以通过左右子节点的指针把整棵树串起来。
利用这种节点结构所得到的二叉树存储结构,叫做二叉链表,一个节点结构中带两个指针。有时候为了方便找到某个节点的父节点,还可以在设计节点结构的时候再增加一个指针,用于指向其父节点,这种节点结构所得到的二叉树存储结构,就叫做三叉链表,也就是一个节点结构中带三个指针。
二叉树顺序存储的常用操作
概念理清之后,我们就要开始代码层面的学习了。虽然顺序存储结构一般是用于存储完全二叉树,但为了让写出的代码也支持普通二叉树,所以我会用二叉树的顺序存储方式,存储图5左侧所示的普通二叉树。
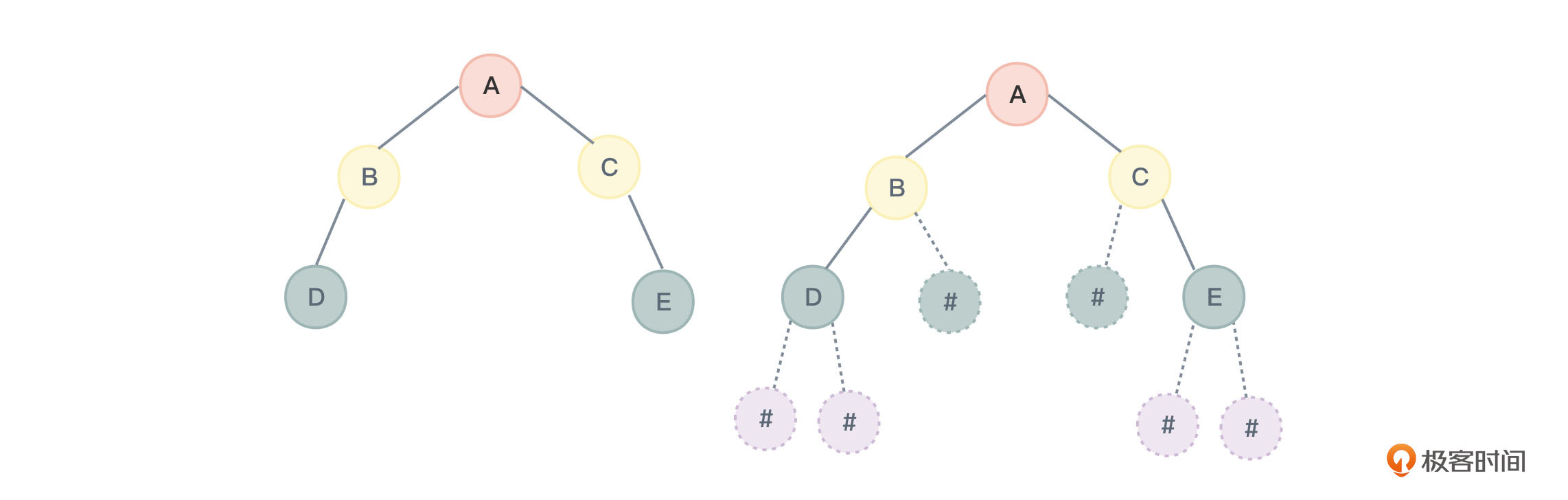
二叉树顺序存储的实现代码参见课件。
在main主函数中,增加如下测试代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| BinaryTree<int> mytree;
//创建一棵二叉树
int indexRoot = mytree.CreateNode(-1, E_Root, 'A'); //创建树根节点A
int indexNodeB = mytree.CreateNode(indexRoot, E_ChildLeft, 'B'); //创建树根的左子节点B
int indexNodeC = mytree.CreateNode(indexRoot, E_ChildRight, 'C'); //创建树根的右子节点C
int indexNodeD = mytree.CreateNode(indexNodeB, E_ChildLeft, 'D'); //创建节点B的左子节点D
int indexNodeE = mytree.CreateNode(indexNodeC, E_ChildRight, 'E'); //创建节点C的右子节点E
int iParentIndexE = mytree.getParentIdx(indexNodeE); //获取某个节点的父节点的下标
cout << "节点E的父节点的下标是:" << iParentIndexE << endl;
int iLevel = mytree.getPointLevel(indexNodeD); //获取某个节点所在的高度
cout << "节点D所在的高度是:" << iLevel << endl;
iLevel = mytree.getPointLevel(indexNodeE);
cout << "节点E所在的高度是:" << iLevel << endl;
cout << "二叉树的深度是:" << mytree.getLevel() << endl;
cout << "二叉树是个完全二叉树吗?" << mytree.ifCompleteBT() << endl;
cout << "------------" << endl;
cout << "前序遍历序列为:";
mytree.preOrder(); //前序遍历
|
代码的执行结果如下。

特别说明,因为在面试和实际应用中,二叉树的链式存储使用得更加频繁,因此许多常用操作我会在下面讲解链式存储中实现,有兴趣的话,你也可以尝试将这些常用操作搬移到二叉树的顺序存储中实现。
二叉树链式存储的常用操作
下面我们熟悉一下二叉树链式存储的常用操作。完整的课件在这里。
类定义、初始化和释放操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| enum ECCHILDSIGN //节点标记
{
E_Root, //树根
E_ChildLeft, //左孩子
E_ChildRight //右孩子
};
//树中每个节点的定义
template <typename T> //T代表数据元素的类型
struct BinaryTreeNode
{
T data; //数据域,存放数据元素
BinaryTreeNode* leftChild, //左子节点指针
* rightChild; //右子节点指针
//BinaryTreeNode* parent; //父节点指针,可以根据需要决定是否引入
};
//二叉树的定义
template <typename T>
class BinaryTree
{
public:
BinaryTree(); //构造函数
~BinaryTree(); //析构函数
public:
//创建一个树节点
BinaryTreeNode<T>* CreateNode(BinaryTreeNode<T>* parentnode, ECCHILDSIGN pointSign, const T& e);
//释放树节点
void ReleaseNode(BinaryTreeNode<T>* pnode);
private:
BinaryTreeNode<T>* root; //树根指针
};
//构造函数
template<class T>
BinaryTree<T>::BinaryTree()
{
root = nullptr;
}
//析构函数
template<class T>
BinaryTree<T>::~BinaryTree()
{
ReleaseNode(root);
};
//释放二叉树节点
template<class T>
void BinaryTree<T>::ReleaseNode(BinaryTreeNode<T>* pnode)
{
if (pnode != nullptr)
{
ReleaseNode(pnode->leftChild);
ReleaseNode(pnode->rightChild);
}
delete pnode;
}
|
创建树节点操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| //创建一个树节点
template<class T>
//参数1:父节点指针,参数2:标记所创建的是树根、左孩子、右孩子,参数3:插入的树节点的元素值
BinaryTreeNode<T>* BinaryTree<T>::CreateNode(BinaryTreeNode<T>* parentnode, ECCHILDSIGN pointSign, const T& e)
{
//将新节点创建出来
BinaryTreeNode<T>* tmpnode = new BinaryTreeNode<T>;
tmpnode->data = e;
tmpnode->leftChild = nullptr;
tmpnode->rightChild = nullptr;
//把新节点放入正确的位置
if (pointSign == E_Root)
{
//创建的是根节点
root = tmpnode;
}
if (pointSign == E_ChildLeft)
{
//创建的是左孩子节点
parentnode->leftChild = tmpnode;
}
else if (pointSign == E_ChildRight)
{
//创建的是右孩子节点
parentnode->rightChild = tmpnode;
}
return tmpnode;
}
|
在main主函数中,加入如下代码,创建一个如前面图5左侧所示的一棵二叉树。
1
2
3
4
5
6
7
8
| BinaryTree<int> mytree;
//创建一棵二叉树
BinaryTreeNode<int>* rootpoint = mytree.CreateNode(nullptr, E_Root, 'A'); //创建树根节点A
BinaryTreeNode<int>* subpoint = mytree.CreateNode(rootpoint, E_ChildLeft, 'B'); //创建树根的左子节点B
subpoint = mytree.CreateNode(subpoint, E_ChildLeft, 'D'); //创建左子节点B下的左子节点D
subpoint = mytree.CreateNode(rootpoint, E_ChildRight, 'C'); //创建树根的右子节点C
subpoint = mytree.CreateNode(subpoint, E_ChildRight, 'E'); //创建右子节点C下的右子节点E
|
在前面讲解扩展二叉树时,你已经知道,给出一个扩展二叉树的前序遍历序列,能够唯一确定一棵二叉树。前面图5中右侧的扩展二叉树,其前序遍历序列是“ABD###C#E##”,那么如果想通过这个遍历序列把这棵二叉树创建,是否可以做到呢?可以。
我们在类模板BinaryTree中增加如下两个成员函数声明。
1
2
3
4
5
6
| public:
//利用扩展二叉树的前序遍历序列来创建一棵二叉树
void CreateBTreeAccordPT(char* pstr);
private:
//利用扩展二叉树的前序遍历序列创建二叉树的递归函数
void CreateBTreeAccordPTRecu(BinaryTreeNode<T>*& tnode, char*& pstr);//参数为引用类型,确保递归调用中对参数的改变会影响到调用者
|
在类模板BinaryTree定义之外,实现上述两个成员函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| //利用扩展二叉树的前序遍历序列来创建一棵二叉树
template<class T>
void BinaryTree<T>::CreateBTreeAccordPT(char* pstr)
{
CreateBTreeAccordPTRecu(root, pstr);
}
//利用扩展二叉树的前序遍历序列创建二叉树的递归函数
template<class T>
void BinaryTree<T>::CreateBTreeAccordPTRecu(BinaryTreeNode<T>* &tnode, char* &pstr)
{
if (*pstr == '#')
{
tnode = nullptr;
}
else
{
tnode = new BinaryTreeNode<T>; //创建根节点
tnode->data = *pstr;
CreateBTreeAccordPTRecu(tnode->leftChild, ++pstr); //创建左子树
CreateBTreeAccordPTRecu(tnode->rightChild, ++pstr);//创建右子树
}
}
|
在main主函数中,注释掉以往的代码,新增如下测试代码。
1
2
| BinaryTree<int> mytree2;
mytree2.CreateBTreeAccordPT((char *)"ABD###C#E##");
|
通过跟踪调试,不难看到,上述的mytree2所存储的数据正是图5左侧所示的二叉树。
遍历操作
二叉树创建出来后,就可以通过前面讲解过的遍历方式,将树中各个节点的内容输出出来以方便观察。我们从深度、广度优先遍历两种方式的角度去了解。
将下列前序、中序、后序遍历的代码加入到类模板BinaryTree的定义中,注意用public修饰。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| //前序遍历二叉树
void preOrder()
{
preOrder(root);
}
void preOrder(BinaryTreeNode<T>* tNode)
{
if (tNode != nullptr) //若二叉树非空
{
//根左右顺序
cout << (char) tNode->data << " "; //输出节点的数据域的值,为方便观察,用char以显示字母
preOrder(tNode->leftChild); //递归方式前序遍历左子树
preOrder(tNode->rightChild); //递归方式前序遍历右子树
}
}
//--------------------------
//中序遍历二叉树
void inOrder()
{
inOrder(root);
}
void inOrder(BinaryTreeNode<T>* tNode) //中序遍历二叉树
{
if (tNode != nullptr) //若二叉树非空
{
//左根右顺序
inOrder(tNode->leftChild); //递归方式中序遍历左子树
cout << (char)tNode->data << " "; //输出节点的数据域的值
inOrder(tNode->rightChild); //递归方式中序遍历右子树
}
}
//--------------------------
//后序遍历二叉树
void postOrder()
{
postOrder(root);
}
void postOrder(BinaryTreeNode<T>* tNode) //后序遍历二叉树
{
if (tNode != nullptr) //若二叉树非空
{
//左右根顺序
postOrder(tNode->leftChild); //递归方式后序遍历左子树
postOrder(tNode->rightChild); //递归方式后序遍历右子树
cout << (char)tNode->data << " "; //输出节点的数据域的值
}
}
|
在main主函数中,继续增加如下代码对刚刚创建的树进行前序、中序和后序遍历。
1
2
3
4
5
6
7
8
9
10
| cout << "前序遍历序列为:";
mytree2.preOrder(); //前序遍历
cout << endl; //换行
cout << "中序遍历序列为:";
mytree2.inOrder(); //中序遍历
cout << endl; //换行
cout << "后序遍历序列为:";
mytree2.postOrder(); //后序遍历
|
新增代码的执行结果如下,正是对图5左侧所示的二叉树进行前序、中序、后序遍历得到的结果。

除了对二叉树进行前序、中序、后序遍历之外,还有一种遍历方式叫层序遍历。前面说过,二叉树的层序遍历需要借助队列来完成,因为难以估计二叉树节点个数,所以使用顺序队列不合适,这里就用链式队列。
我们把以往讲解的链式队列相关的代码复制到本项目当前的MyProject.cpp文件中来。将下列代码加入到类模板BinaryTree的定义中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| //--------------------------
//层序遍历二叉树
void levelOrder()
{
levelOrder(root);
}
void levelOrder(BinaryTreeNode<T>* tNode)
{
if (tNode != nullptr) //若二叉树非空
{
BinaryTreeNode<T>* tmpnode;
LinkQueue<BinaryTreeNode<T>*> lnobj;//注意,队列的元素类型是“节点指针”类型
lnobj.EnQueue(tNode); //先把根节点指针入队
while (!lnobj.IsEmpty()) //循环判断队列是否为空
{
lnobj.DeQueue(tmpnode); //出队列
cout << (char)tmpnode->data << " ";
if(tmpnode->leftChild != nullptr)
lnobj.EnQueue(tmpnode->leftChild); //左孩子入队
if (tmpnode->rightChild != nullptr) //右孩子入队
lnobj.EnQueue(tmpnode->rightChild);
} //end while
}
}
|
在main主函数中,继续增加如下代码对刚刚创建的树进行层序遍历。
1
2
3
| cout << endl; //换行
cout << "层序遍历序列为:";
mytree2.levelOrder();
|
新增代码的执行结果如下。

这里可以进一步思考一下,如何在上述层序遍历代码中加入一些代码来判断二叉树是否是一棵完全二叉树呢?
如果某个节点的左子节点不存在而右子节点存在,那么这棵二叉树就不是完全二叉树,所以上述层序遍历代码中,在出队列一个节点后,可以加入如下代码来判断一棵二叉树是否是完全二叉树。
1
2
3
4
| if(tmpnode->leftChild == nullptr && tmpnode->rightChild != nullptr)
{
//这棵二叉树不是一棵完全二叉树。
}
|
上述无论何种遍历方式,每个节点被访问的次数都是有限的,所以遍历操作的时间复杂度和二叉树的节点个数成正比,即二叉树遍历的时间复杂度为O(n)。
其他常用操作
最后,我们将分别实现二叉树的一些常用操作,包括计算节点个数、求二叉树的高度、根据给的节点值查找某个节点、查找某个节点的父节点、二叉树的拷贝。这些代码都可以在类模板BinaryTree的定义中实现。
1
2
3
4
5
6
7
8
9
10
11
12
| //求二叉树节点个数
int getSize()
{
return getSize(root);
}
int getSize(BinaryTreeNode<T>* tNode) //也可以用遍历二叉树的方式求节点个数
{
if (tNode == nullptr)
return 0;
return getSize(tNode->leftChild) + getSize(tNode->rightChild) + 1; //之所以+1,是因为还有个根节点
}
|
增加下列测试代码(在main主函数中),确保增加的操作能够正常运行。
1
| cout << "二叉树节点个数为:" << mytree2.getSize() << endl;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| //求二叉树高度(取左右子树中高度更高的)
int getHeight()
{
return getHeight(root);
}
int getHeight(BinaryTreeNode<T>* tNode)
{
if (tNode == nullptr)
return 0;
int lheight = getHeight(tNode->leftChild); //左子树高度
int rheight = getHeight(tNode->rightChild); //右子树高度
if (lheight > rheight)
return lheight + 1 ; //之所以+1,是因为还包括根节点的高度
return rheight + 1; //之所以+1,是因为还包括根节点的高度
}
|
增加下列测试代码。
1
| cout << "二叉树的高度为:" << mytree2.getHeight() << endl;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| BinaryTreeNode<T>* SearchElem(const T& e)
{
return SearchElem(root, e);
}
BinaryTreeNode<T>* SearchElem(BinaryTreeNode<T>* tNode,const T& e)
{
if (tNode == nullptr)
return nullptr;
if (tNode->data == e) //从根开始找
return tNode;
BinaryTreeNode<T>* p = SearchElem(tNode->leftChild, e); //查找左子树
if (p != nullptr) //这里的判断不可缺少
return p;
return SearchElem(tNode->rightChild, e); //左子树查不到,继续到右子树查找,这里可以直接return
}
|
增加下列测试代码。
1
2
3
4
5
6
7
| //查找某个节点
int val = 'B';
BinaryTreeNode<int>* p = mytree2.SearchElem(val);
if (p != nullptr)
cout << "找到了值为" << (char)val << "的节点" << endl;
else
cout << "没找到值为" << (char)val << "的节点" << endl;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| BinaryTreeNode<T>* GetParent(BinaryTreeNode<T>* tSonNode)
{
return GetParent(root, tSonNode);
}
BinaryTreeNode<T>* GetParent(BinaryTreeNode<T>* tParNode, BinaryTreeNode<T>* tSonNode)
{
if (tParNode == nullptr || tSonNode == nullptr)
return nullptr;
if (tParNode->leftChild == tSonNode || tParNode->rightChild == tSonNode)
return tParNode;
BinaryTreeNode<T>* pl = GetParent(tParNode->leftChild, tSonNode);
if (pl != nullptr)
return pl;
return GetParent(tParNode->rightChild, tSonNode);
}
|
增加下列测试代码。
1
2
3
4
5
6
| //查找某个节点的父节点
BinaryTreeNode<int>* parp = mytree2.GetParent(p);
if (parp != nullptr)
cout << "找到了值为" << (char)val << "的节点的父节点" << (char)parp->data << endl;
else
cout << "没找到值为" << (char)val << "的节点的父节点" << endl;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| void CopyTree(BinaryTree<T>* targetTree)
{
CopyTree(root,targetTree->root);
}
void CopyTree(BinaryTreeNode<T>* tSource,BinaryTreeNode<T>* &tTarget) //注意第二个参数类型为引用
{
if (tSource == nullptr)
{
tTarget = nullptr;
}
else
{
tTarget = new BinaryTreeNode<T>;
tTarget->data = tSource->data;
CopyTree(tSource->leftChild, tTarget->leftChild); //对左子树进行拷贝
CopyTree(tSource->rightChild, tTarget->rightChild);//对右子树进行拷贝
}
}
|
增加下列测试代码。
1
2
3
| //测试树的拷贝
BinaryTree<int> mytree3;
mytree2.CopyTree(&mytree3);
|
非递归遍历操作
在前面的二叉树遍历代码实现中,除层序遍历外,前序、中序、后序遍历采用的都是递归方式来实现的,这种实现方法代码比较简单。但实际的面试中,有时也会要求采用非递归的方式实现前序、中序、后序遍历,这往往需要借助栈来实现。并且实际的应用中,如果二叉树的高度特别高,节点特别多,用递归的方式遍历可能会导致栈溢出,此时就需要采用非递归方式遍历了。
把[第10节课]提到的链式栈相关代码复制到当前的MyProject.cpp文件中来。非递归遍历代码都可以在类模板BinaryTree的定义中实现。

你可以根据图片提示,自己手工绘制一下入栈和出栈的过程,这样也会对通过栈实现前序遍历有一个更深刻的认识。
我们把以往讲解的链式栈相关的代码复制到本项目当前的MyProject.cpp文件中来。将下列代码加入到类模板BinaryTree的定义中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| //非递归方式前序遍历二叉树
void preOrder_noRecu()
{
preOrder_noRecu(root);
}
void preOrder_noRecu(BinaryTreeNode<T>* tRoot)
{
if (tRoot == nullptr)
return;
LinkStack< BinaryTreeNode<T>* > slinkobj;
slinkobj.Push(tRoot); //根节点入栈
BinaryTreeNode<T>* tmpnode;
while (!slinkobj.Empty()) //栈不空
{
slinkobj.Pop(tmpnode); //栈顶元素出栈
cout << (char)tmpnode->data << " "; //访问栈顶元素
if (tmpnode->rightChild != nullptr) //注意先判断右树再判断左树
{
slinkobj.Push(tmpnode->rightChild); //把右树入栈
}
if (tmpnode->leftChild != nullptr)
{
slinkobj.Push(tmpnode->leftChild); //把左树入栈
}
} //end while
}
|
增加下列测试代码。
1
2
3
| cout << "非递归方式前序遍历序列为:";
mytree2.preOrder_noRecu();
cout << endl;
|
新增代码的执行结果如下。


相应的代码我也放在了下面,不过写法不限于这一种,有兴趣可以发挥自己的想象力,根据“左根右”这个遍历顺序写出不同的非递归遍历代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| //非递归方式中序遍历二叉树
void inOrder_noRecu()
{
inOrder_noRecu(root);
}
void inOrder_noRecu(BinaryTreeNode<T>* tRoot)
{
if (tRoot == nullptr)
return;
LinkStack< BinaryTreeNode<T>* > slinkobj;
slinkobj.Push(tRoot);//根节点入栈
BinaryTreeNode<T>* tmpnode;
while (!slinkobj.Empty()) //栈不空
{
while (tRoot->leftChild != nullptr)
{
slinkobj.Push(tRoot->leftChild); //将“当前节点的左节点”入栈
tRoot = tRoot->leftChild; //将“当前节点的左节点”重新标记为当前节点。
} //end while
slinkobj.Pop(tmpnode); //对栈顶元素出栈(同时获取了栈顶元素)
cout << (char)tmpnode->data << " ";
//查看右树
if (tmpnode->rightChild != nullptr)
{
tRoot = tmpnode->rightChild; //将刚刚从栈顶出栈的元素的右节点标记为当前节点
slinkobj.Push(tRoot); //右节点入栈
}
}//end while
}
|
增加下列测试代码。
1
2
3
| cout << "非递归方式中序遍历序列为:";
mytree2.inOrder_noRecu();
cout << endl;
|
新增代码的执行结果如下。

后序遍历的实现比前序和中序遍历更繁琐一些。因为后序遍历的顺序是“左右根”,也就是说,是否访问某个节点,取决于当前访问完毕的是该节点的左子树还是右子树。
如果是左子树访问完毕,根据“左右根”的遍历顺序,必须去访问右子树,如果是右子树访问完毕,则就可以去访问该根节点。
因此,要实现这里的后序遍历,当将一个节点入栈的时候,必须同时标记后续入栈的是该节点的左子树还是右子树,这意味着需要将“节点指针和标记”同时入栈和出栈。
所以,前面代码中定义的用于表示树中每个节点的BinaryTreeNode类模板中,缺少了一个标记字段用来标记左右子树。
为了实现非递归后序遍历,可以考虑扩充BinaryTreeNode类模板的定义,也就是增加一个左右节点的标记,也可以定义一个新的类模板增加一个左右节点的标记,并将BinaryTreeNode类模板包含在其中。
这里采用后一种实现方式——在BinaryTreeNode类模板的实现代码之下,增加新的类模板BTNode_extra,实现代码如下。
1
2
3
4
5
6
7
| //为实现二叉树的非递归后序遍历引入的新类模板
template <typename T> //T代表数据元素的类型
struct BTNode_extra
{
BinaryTreeNode<T> * point;
ECCHILDSIGN pointSign;
};
|
在这里先把后序遍历的过程描述一下。

非递归方式后序遍历二叉树的代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| //非递归后序遍历二叉树
void postOrder_noRecu()
{
postOrder_noRecu(root);
}
void postOrder_noRecu(BinaryTreeNode<T>* tRoot)
{
if (tRoot == nullptr)
return;
LinkStack< BTNode_extra<T> > slinkobj;
BTNode_extra<T> ext_tmpnode;
do
{
while (tRoot != nullptr)
{
ext_tmpnode.point = tRoot;
ext_tmpnode.pointSign = E_ChildLeft; //标记先处理该节点的左孩子
slinkobj.Push(ext_tmpnode);
tRoot = tRoot->leftChild;
}
while (!slinkobj.Empty())
{
slinkobj.Pop(ext_tmpnode); //出栈
if (ext_tmpnode.pointSign == E_ChildLeft)
{
//把左标记更改为右标记
ext_tmpnode.pointSign = E_ChildRight; //标记该节点的右孩子
slinkobj.Push(ext_tmpnode); //重新入栈
tRoot = ext_tmpnode.point->rightChild;
break; //终止while循环
}
else //if (ext_tmpnode.pointSign == E_ChildRight) 肯定是右子树标记,所以这个if不需要
{
//根据左右根规则,右节点之后可以访问根节点
cout << (char)ext_tmpnode.point->data << " ";
}
} //end while
} while (!slinkobj.Empty());
}
|
增加下列测试代码。
1
2
3
| cout << "非递归方式后序遍历序列为:";
mytree2.postOrder_noRecu();
cout << endl;
|
新增代码的执行结果如下。

通过遍历序列创建二叉树
前面我们说过一个结论:已知前序和中序遍历序列,能够唯一确定一棵二叉树。那么,是否可以实现一个这样的成员函数,用来实现这棵二叉树的创建呢?
完全可以。在BinaryTree类模板的定义中实现,代码如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| //如何根据前序、中序遍历序列来创建一棵二叉树呢?
//pP_T:前序遍历序列,比如是“ABDCE”,pI_T:中序遍历序列,比如是“DBACE”
void CreateBTreeAccordPI(char* pP_T, char* pI_T)
{
CreateBTreeAccordPI(root, pP_T, pI_T, strlen(pP_T));
}
void CreateBTreeAccordPI(BinaryTreeNode<T>*& tnode, char* pP_T,char * pI_T,int n)//参数1为引用类型,确保递归调用中对参数的改变会影响到调用者,n:节点个数
{
if (n == 0)
{
tnode = nullptr;
}
else
{
//(1)在中序遍历序列中找根,前序遍历序列中根在最前面
int tmpindex = 0; //下标
while (pP_T[0] != pI_T[tmpindex])
++tmpindex;
tnode = new BinaryTreeNode<T>; //创建根节点
tnode->data = pI_T[tmpindex]; //第一次tmpindex=2
//(2)创建左孩子
CreateBTreeAccordPI(
tnode->leftChild, //创建左孩子
pP_T + 1, //找到前序遍历序列中左树开始节点的位置,这里跳过第一个(根)节点A,得到的是“BDCE”
pI_T, //不需要改动,仍旧是“DBACE”
tmpindex //左孩子有2个节点
);
//(3)创建右孩子
CreateBTreeAccordPI(
tnode->rightChild, //创建右孩子
pP_T + tmpindex + 1, //找到前序遍历系列中右树开始节点的位置,不难发现,前序遍历序列和中序遍历序列右树开始节点的位置相同,得到的是“CE”
pI_T + tmpindex + 1, //找到中序遍历系列中右树开始节点的位置。得到的是“CE”
n - tmpindex - 1 //右孩子节点数
);
}
}
|
在main主函数中,把如下创建二叉树的代码行。
1
| mytree2.CreateBTreeAccordPT((char *)"ABD###C#E##");
|
替换为新的代码行来创建一棵图5左侧所示的二叉树。
1
| mytree2.CreateBTreeAccordPI((char*)"ABDCE", (char*)"DBACE");
|
发现二叉树创建成功。
小结
这节课,我们学习了二叉树的两种存储方式——顺序存储方式、链式存储方式,以及他们的实现方式。
二叉树的顺序存储,是用一段连续的内存依次从上到下从左到右存储二叉树各个节点元素,但是很容易造成存储空间的浪费,因此顺序存储往往比较适合存储完全二叉树。
二叉树的链式存储,需要存储额外的左右节点指针。虽然增加了存储的灵活性,但也消耗了更多的存储空间。链式存储方式中,还涉及到了二叉链表和三叉链表的概念。二叉链表的一个节点结构带有两根指针以指向左右孩子节点,而三叉链表中一个节点结构带有三根指针,其中第三个指针用于指向当前节点的父节点,这给找当前节点的父节点带来了最大的便利。
由于与顺序存储相比,二叉树链式存储更加常用,所以这节课我将重点放在了二叉树链式存储的常用操作。给出了创建树节点,获取二叉树的前序、中序、后序、层序遍历序列,获取二叉树节点个数,获取二叉树高度,查找某个节点,查找某个节点的父节点,树的拷贝等操作代码。这里要重点记忆二叉树前序、中序、后序遍历代码,理解性记忆层序遍历代码,以防在面试中出现。
此外,我们也利用非递归的编程方式实现了二叉树的前序、中序、后序遍历。注意,非递归的遍历操作需要借助栈来实现。这些代码需要我们简单理解、适当记忆,万一面试中出现,能说上几句就是好的。
最后,如何从无到有创建出一棵二叉树来呢?我们在最后用前序、中序遍历序列创建了一棵二叉树,这些代码都不复杂,但一定可以作为参考和借鉴,帮助你进一步拓展创建二叉树的思路。
课后思考
已知“中序和后序遍历序列”,也能够唯一确定一棵二叉树,请你尝试实现相关代码。
欢迎在留言区分享你的成果代码。如果觉得有所收获,也可以把课程分享给更多的朋友一起学习。我们下节课见!













