你好,我是王健伟。
这节课我们学习图的应用中的最后一个话题——关键路径问题。它解决的事估算完成某个工程所需要的最短时间的问题。说到“最短时间”,你应该就能反应过来,它是一个能帮助我们提高生产效率的算法。
我们还是从它涉及的基本概念开始说起。
“关键路径”都涉及什么基本概念?
前面介绍了AOV网,我们先回顾一下它的概念:有向图(无权值的)中若以顶点表示活动,有向边(弧)表示活动之间的先后关系,这样的有向图称为顶点表示活动的网,简称为AOV网。
这里引入与AOV网相对应的另一个概念:AOE网(Activity On Edge Network)。
什么意思呢?在一个表示工程的带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销或该活动的持续时间,这样的有向图称为边表示活动的网,简称AOE网。
这里有几个你需要理解的AOE网的性质。
- 只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始。
- 只有在进入某顶点的各有向边所代表的活动都结束时,该顶点所代表的事件才能发生。
- 有些活动是可以并行进行的,有些活动是要分先后的。
单看这些性质不是很好理解,我还是以做一盘番茄炒蛋菜为例,现在要估算做一盘番茄炒蛋菜最短需要多少时间。我们假设做菜的师傅有很多位,这盘番茄炒蛋菜的制作过程由多位师傅同时进行。我们梳理一下每个步骤需要的时间。
- 洗番茄需要3分钟。
- 切番茄需要2分钟。
- 打鸡蛋需要2分钟。
- 鸡蛋中加调料需要1分钟。
- 炒菜需要8分钟。
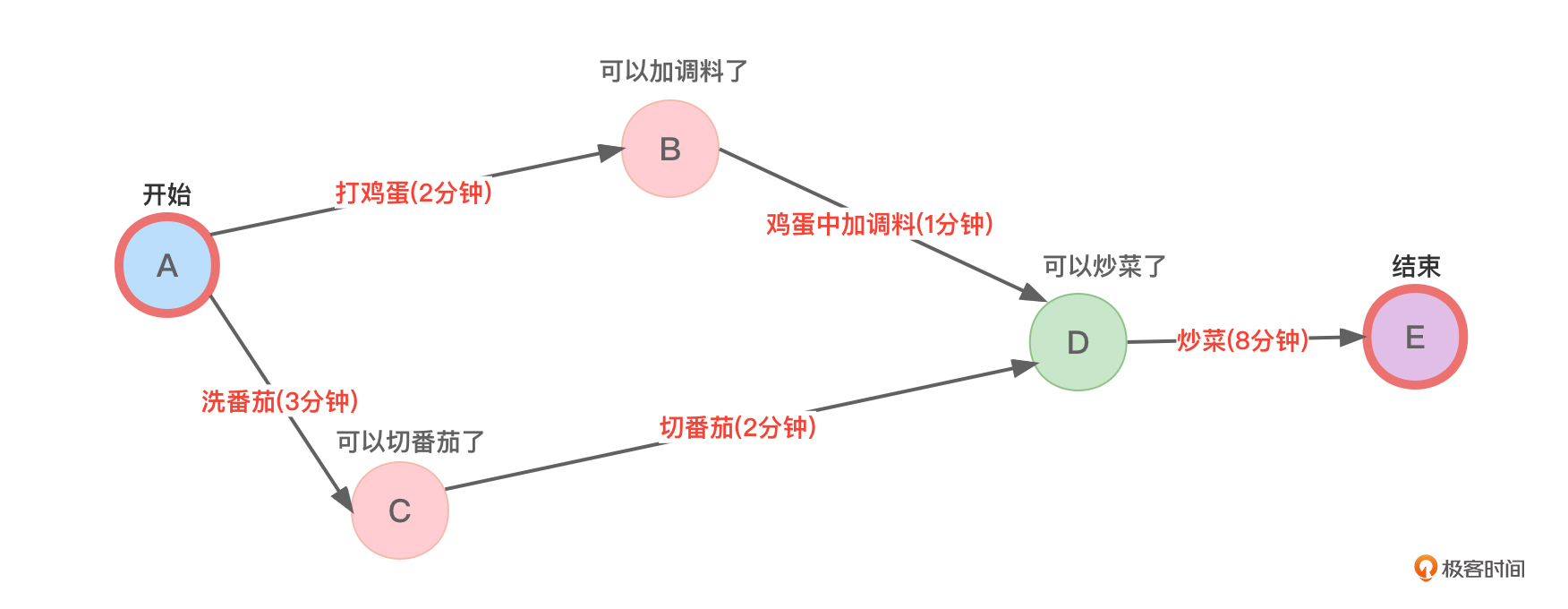
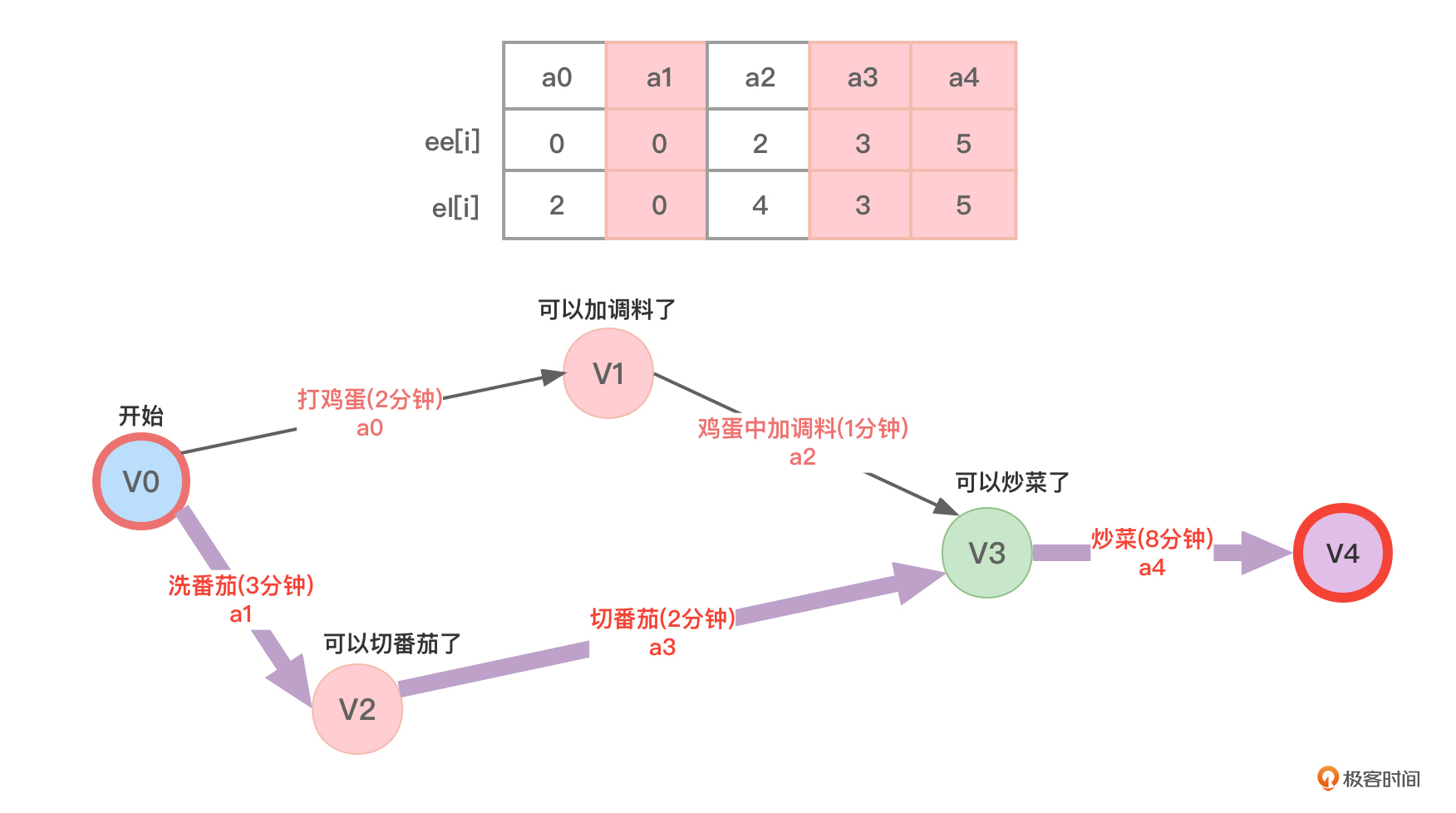
在图1所示的AOE网中,对照一下AOE网的性质。这里注意两点。
- 只有“鸡蛋中加调料”和“切番茄”所代表的活动都结束时,“可以炒菜了”这个顶点所代表的事件才能发生。
- 因为做菜过程中有很多位师傅同时进行,所以“打鸡蛋”和“洗番茄”的过程可以互不相关,也就是性质中的“并行进行”。但“洗番茄”和“切番茄”不能同时进行,这两件事是有先后顺序要分先后来做的,你可以理解成这里只有一个番茄,没洗完不能切。
在AOE网中只有一个入度为0的顶点,称为开始顶点(始点/源点),代表着整个工程的开始。也只有一个出度为0的顶点,称为结束顶点(终点/汇点),代表整个工程的结束。
因为AOE网中有些活动是可以并行进行的,所以完成整个工程需要的最短时间是从开始顶点到结束顶点的最长路径长度,也就是有向边权值之和最大。而这个最长路径长度就叫做关键路径,当然,关键路径可能不只一条。
在图1中,从开始顶点到结束顶点的路径有2条,分别是A,B,D,E和A,C,D,E,第一条路径需要花费的时间总长度是2+1+8=11分钟,第二条路径需要花费的时间总长度是3+2+8=13分钟,显然,第二条路径的长度更长因此是图1的关键路径。
我们把关键路径上的活动称为关键活动,关键活动的时间如果延长,那么整个工程的完成时间也会延长。
所以,AOE网可以回答这么两个问题。
- 完成整个工程需要多少时间?
- 哪些活动是影响工程进度的关键活动?或者说,要缩短完成工程所需要的时间,应该加快哪些活动?
为了更好地编程实现关键路径求解问题,我们还是要引入一些与关键活动有关的概念。为了方便描述,假设AOE网中顶点用v表示,那么这里有4个关键点,分别是事件vk的最早发生时间ve[k]、事件vk的最迟发生时间vl[k]、活动ai的最早开始时间ee[i]以及活动ai的最晚开始时间el[i]。我们一个一个来说。
关键点1:事件vk的最早发生时间ve[k]
这里的字母v即vertex,图的顶点,注意AOE网中图的顶点代表事件;而字母e理解为earliest occurrence time,最早发生时间。
ve[k]指从开始顶点v0到顶点vk的最大路径长度。它的长度决定了从顶点vk发出的活动能够开工的最早时间,也就是说所有以vk为尾的弧表示的是活动的最早开始时间。
那么,如何计算ve[k]呢?我来说下具体的思路。
- 将开始顶点的ve[0]值设置为0(初始值)。
- 思考ve[k]值是多少。
考察指向该顶点的所有弧。针对每条弧都计算出弧尾对应的顶点的ve值+弧长度值所得的和值。选取所有弧中这个和值最大的值作为ve[k]的值。
将图1的各个顶点和边重新编一下号方便描述,如图2所示:
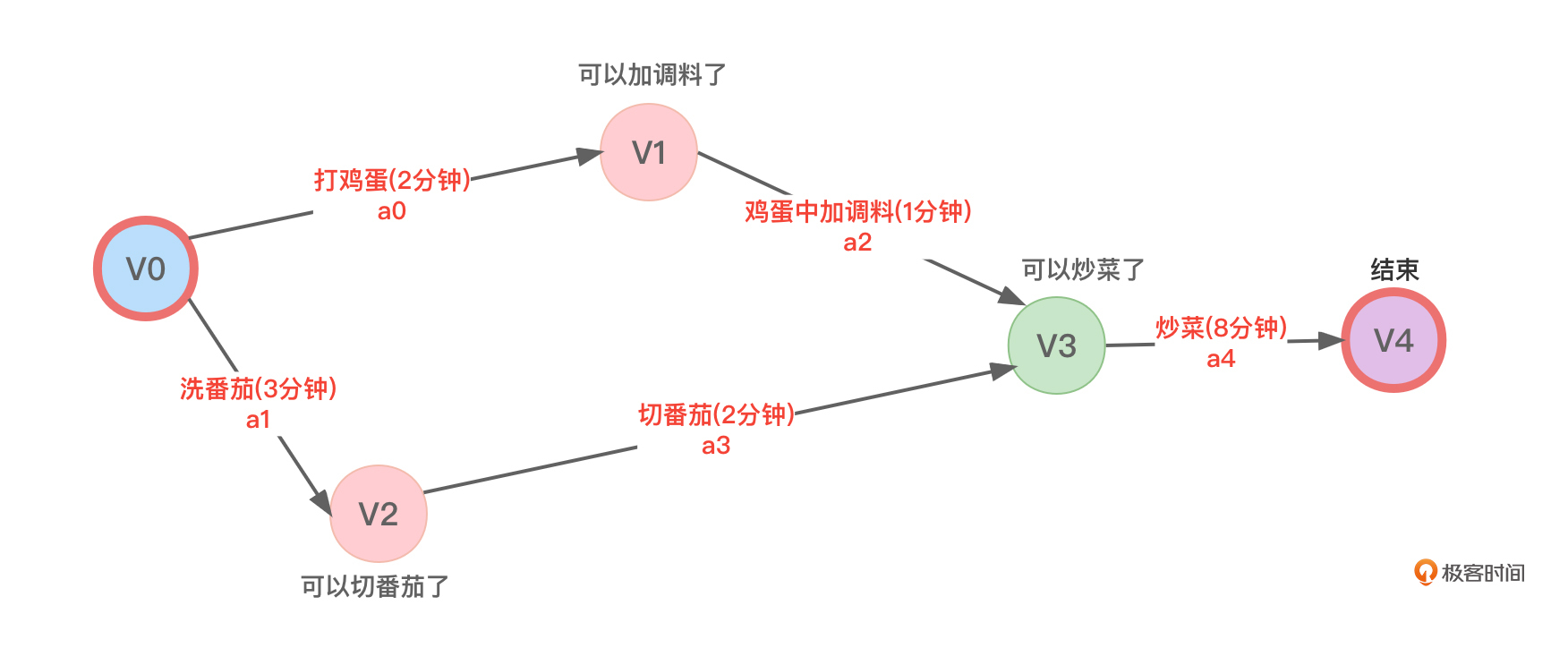
在图2中,ve[0]=0,ve[1]= ve[0]+2=2,ve[2]= ve[0]+3=3。
指向v3顶点的弧有两条,分别是“鸡蛋中加调料(1分钟)”和“切番茄(2分钟)”,这两条弧的弧尾对应的分别是V1顶点和V2顶点:

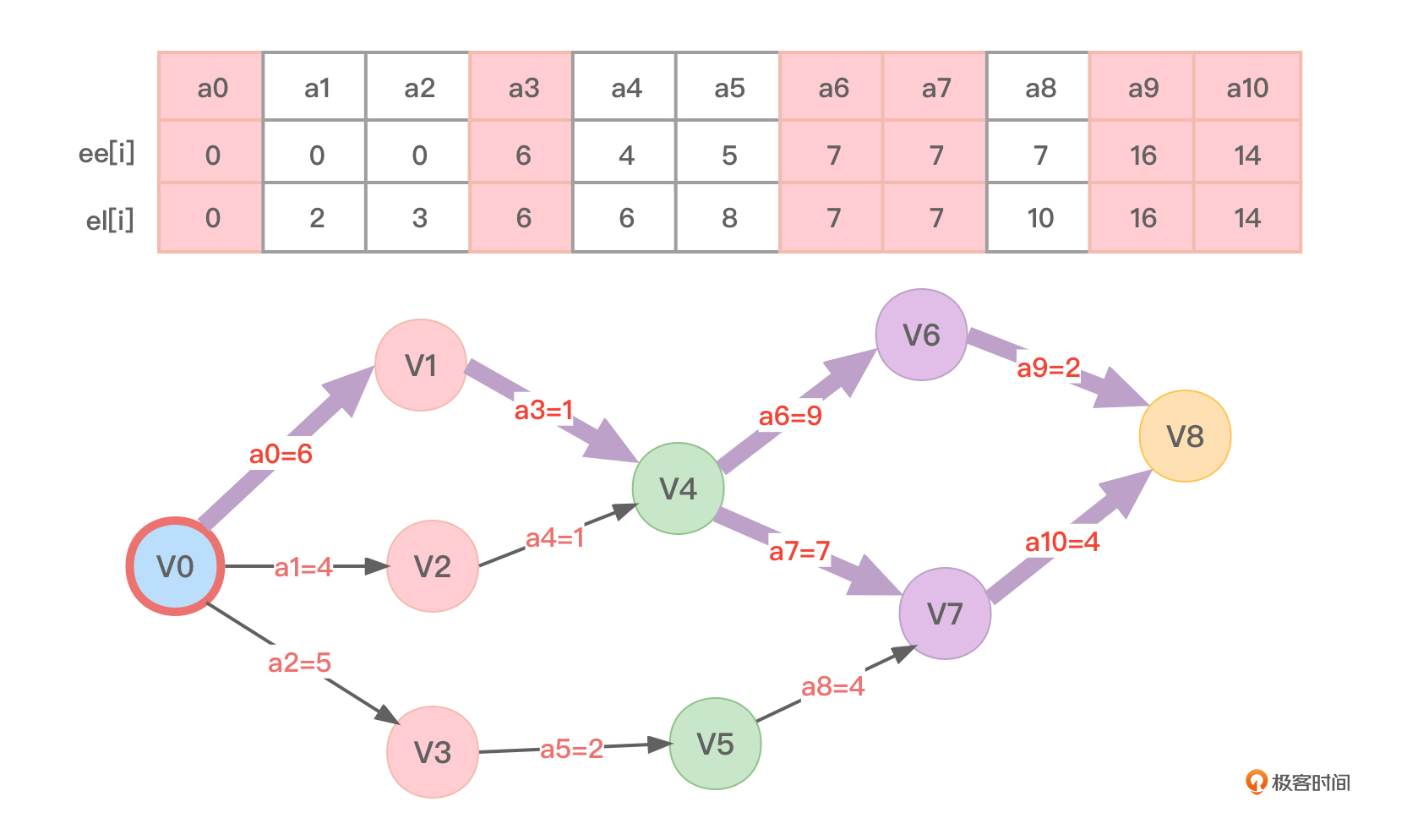
再看一个更复杂的有向无环图对应的AOE网,如图3所示:
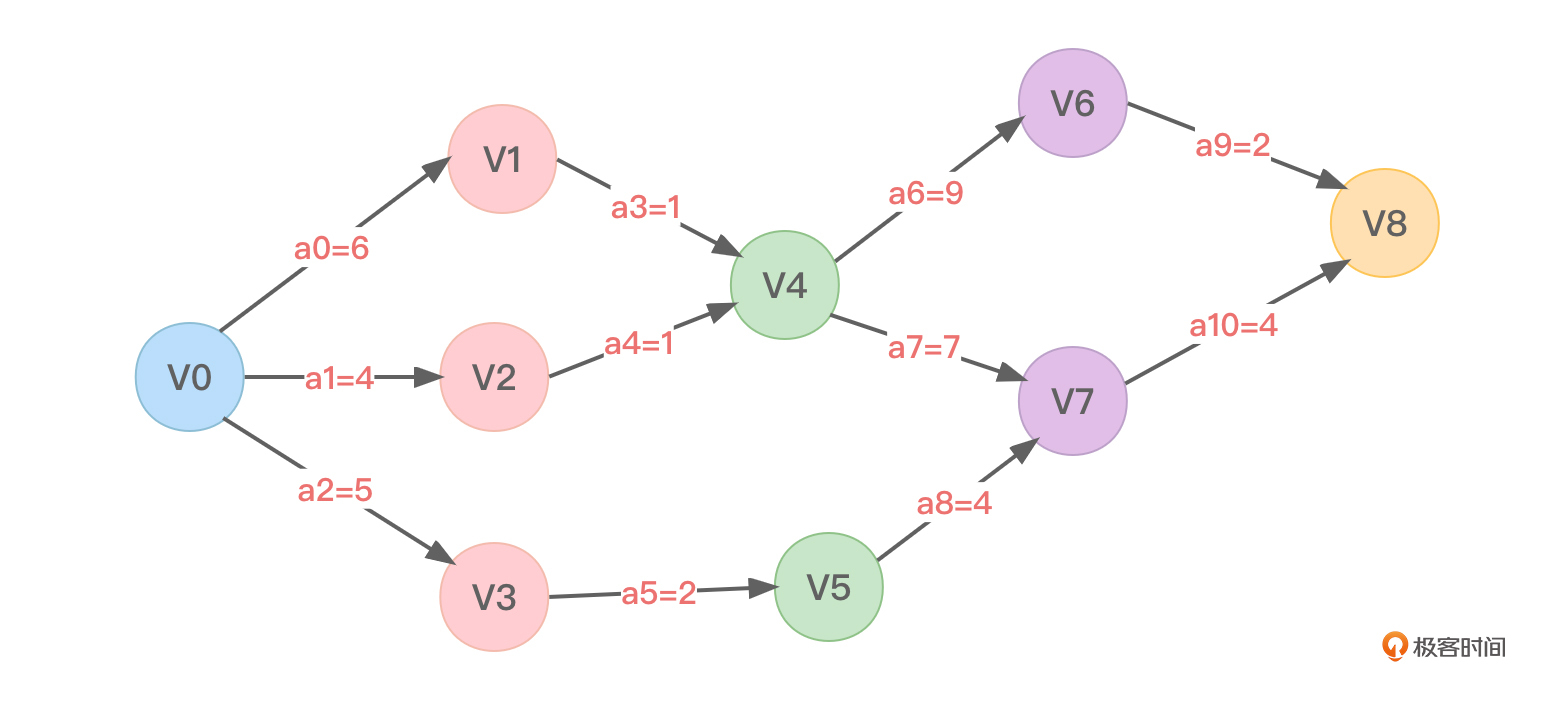
在图3中,看一看每个事件的最早发生时间:

关键点2:事件vk的最迟发生时间vl[k]
这里的字母v即vertex,图的顶点,注意AOE网中图的顶点代表事件;而字母l可以理解为latest occurrence time,最迟发生时间。
vl[k]指不推迟整个工程完成时间(工期)的前提下,事件vk允许的最晚发生时间。
如何计算vl[k]呢?看一下具体的思路。
- 将结束顶点的vl(结束事件最迟发生时间)值初始化为该顶点的ve(结束事件最早发生时间),即vl[n-1]=ve[n-1]。这里假设n代表AOE网顶点数量,顶点的下标从0开始。
- vl[k]是多少呢?这需要从后向前来推算每个顶点的vl值。
考察从该顶点发出的所有弧,这些弧的弧头所指向的顶点显然是已经计算出了vl值的。针对每条弧的弧头所指向的顶点的vl值-弧长度值所得的差值。选取所有弧中这些差值最小的作为vl[k]的值。
在图2中,因为ve[4]=13(前面计算过),所以vl[4]=13。

再看图3,看一看每个事件的最迟发生时间:

关键点3:活动ai的最早开始时间ee[i]
这里的第一个字母e即edge,图的有向边/弧,注意AOE网中图的有向边代表活动;而第二个字母e可以理解为earliest start time,最早开始时间。
活动ai的最早开始时间ee[i]等于该活动所对应的弧尾部所连接的事件(顶点)的最早发生时间ve。以图4来说明:
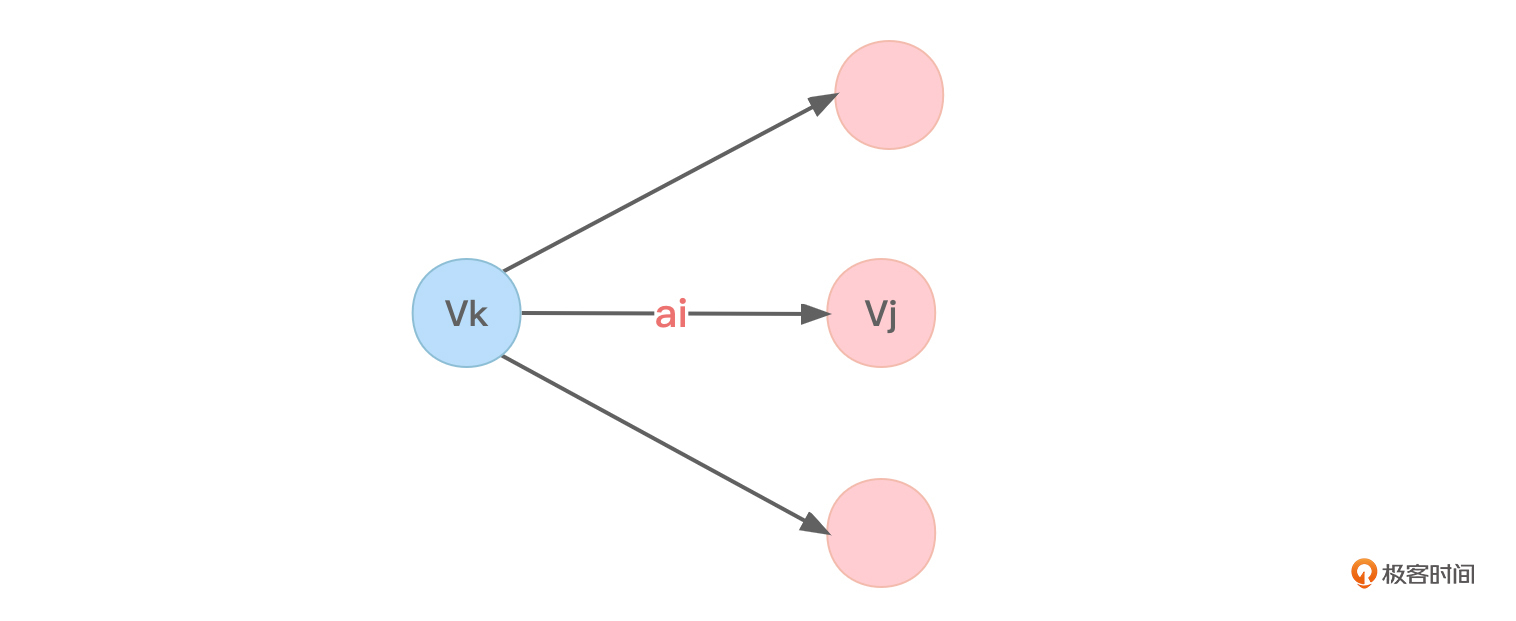
从图4不难看到,ee[i] = ve[k]。
以图2为例,得到的各个活动的最早开始时间为:

以图3为例,得到各个活动的最早开始时间为:

关键点4:活动ai的最晚开始时间el[i]
这里的第一个字母e即edge,图的有向边/弧,注意AOE网中图的有向边代表活动;而第二个字母l理解为latest start time,最晚开始时间。
参考之前的图4,活动ai的最晚开始时间必须要保证事件Vj的最迟发生时间不拖后。所以,活动ai的最晚开始时间el[i]=vl[j]-弧ai的长度值。
以图2为例,得到的各个活动的最晚开始时间为:

怎么解释呢?因为洗番茄需要3分钟,切番茄需要2分钟。而鸡蛋中加调料需要1分钟,所以打鸡蛋这个活动只要不超过4分钟,就不会推迟整个番茄炒蛋菜的完成时间,因为打鸡蛋这个活动需要2分钟,因此4-2=2意味着打鸡蛋这个活动向后拖2分钟是不会耽误整个工程进度的。

以图3为例,得到各个活动的最晚开始时间为:

利用求得的ee和el值就可以求得关键路径:只要将ee和el值相同的项找出来,对于图2,关键路径如图5,即a1、a3、a4:
对于图3,关键路径如图6,即a0、a3、a6、a7、a9、a10,不难看到,这是两条关键路径:
从上面的图中可以看到,只要是活动最早开始时间和活动最晚开始时间相等的项,就属于关键路径上的活动。因为这种活动是属于没有办法推迟必须立即开始干的活动,那么这些活动所连接起来的路径一定是最长的路径,即关键路径。关键路径找到了,那么关键路径上的(关键)活动就找到了。
这里我强调两点。
- 关键路径就是工程中需要花费时间最多的路径,如果对这些关键活动进行优化,比如增派人手,提升速度等,那么整个工程的效率就能得到进一步增强。但是要注意,只有AOE网中关键路径不发生改变的前提下,这些优化才有意义。如果因为优化导致关键路径发生了改变,比如关键活动变成了非关键活动,那么这些优化就失去了意义,所以优化是有限度的,并不是可以无限优化的。
- 如果AOE网中存在多条关键路径(如图6),那么要提高工程的效率来缩短总工程时间就必须同时提高这几条关键路径上的关键活动速度才行。
关键路径算法实现
理清思路之后,我们来说算法的具体实现。这里注意两点:只有带权有向无环图才能求关键路径;通过关键路径算法可以找出关键活动——不按期完成会影响整个工程进度的活动。
关键路径算法的实现思路还是比较清晰的,利用前面讲述的拓扑排序算法确定图中是否有环。在没有环的前提下,计算出事件的最早发生时间ve、事件的最迟发生时间vl、活动的最早开始时间ee,活动的最晚开始时间el,此时,用el-ee求得差值,差值为0的就是关键活动。
el-ee的差值也叫做时间余量,表示在不增加整个工程完成工期的情况下,活动可以拖延的时间。时间余量为0就表示该活动必须按期完成,这样的活动也就是关键活动。由这些关键活动组成的路径就是关键路径。
实现关键路径算法,既可以使用邻接矩阵又可以使用邻接表来保存图,当然,采用其他存储方式也行。这里我采用的是邻接表的方式保存图。考虑到编程的方便,为代码中表示边的节点结构EdgeNode增加“权值”成员变量weight,为表示顶点的节点结构VertexNode增加“入度”成员变量indegree和“出度”成员变量outdegree。
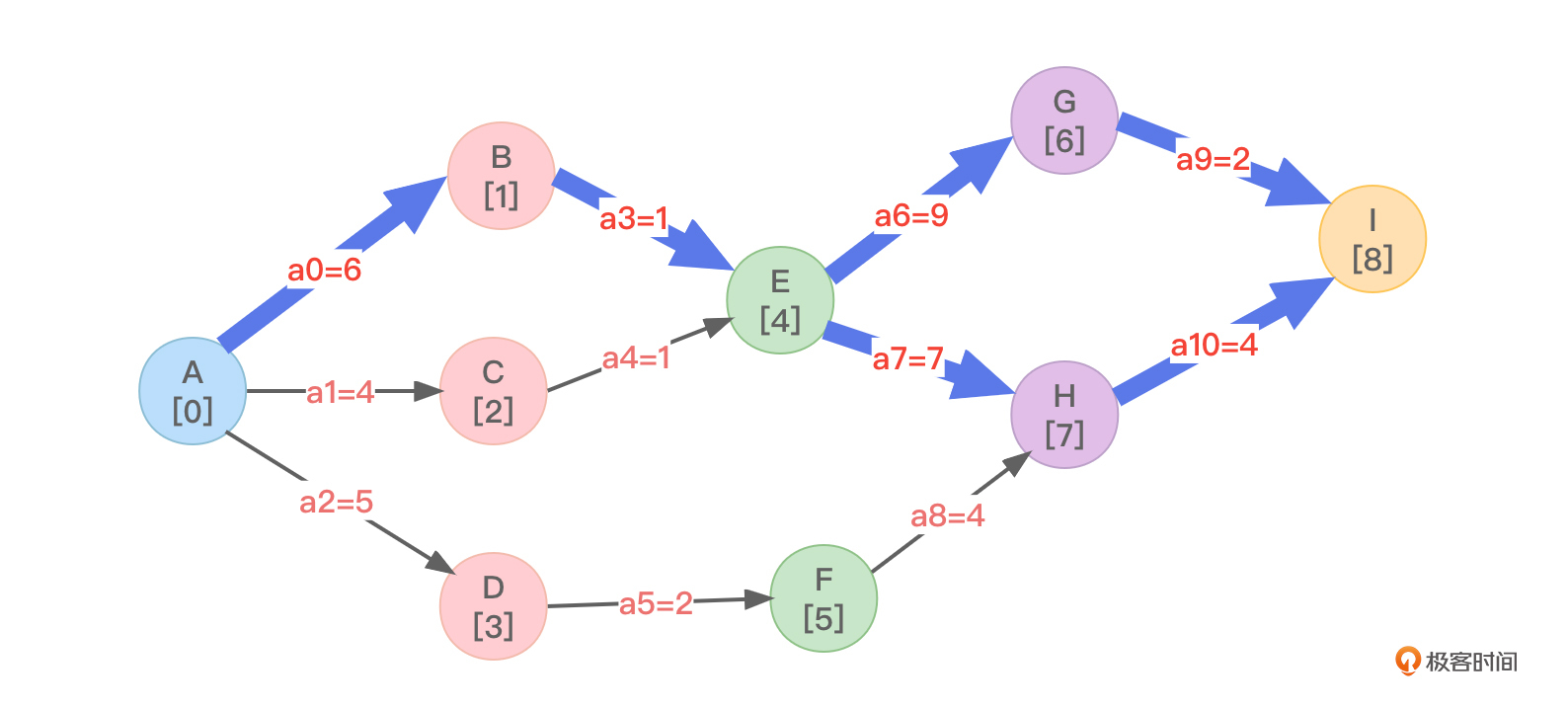
我们参照图7实现关键路径算法的编写。注意,图中顶点进行了重新命名,[ ]中代表该顶点的下标/编号,同时绘制出了图对应的邻接表:

下面就是采用邻接表的方式保存图并求得关键路径的实现源码了。大致的思路就是,通过前述的拓扑排序算法得到了事件的最早发生时间ve值,然后求得事件的最迟发生时间vl值,再求得活动的最早开始时间ee和活动的最晚开始时间el并进行比较,从而确定出关键路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #define MaxVertices_size 10 //最大顶点数大小
//表示边的节点结构
struct EdgeNode
{
int curridx; //边所对应的顶点下标值
int weight; //权值
EdgeNode* next; //指向下一条边
};
//表示顶点的节点结构,其后是一个链表,链表中每个节点都代表着和该顶点相连的边
template<typename T> //T代表顶点类型
struct VertexNode
{
int indegree; //入度
int outdegree; //出度
T data; //顶点中的数据
EdgeNode* point; //指向第一个边节点的指针
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
| //邻接表代表的图
template<typename T> //T代表顶点类型
class GraphLink
{
public:
GraphLink() //构造函数
{
m_numVertices = 0;
m_numEdges = 0;
for (int i = 0; i < MaxVertices_size; ++i)
{
m_VertexArray[i].point = nullptr; //指针可以率先指向nullptr
m_VertexArray[i].outdegree = 0; //出度先给0
m_VertexArray[i].indegree = 0; //入度先给0
}
}
~GraphLink() //析构函数
{
for (int i = 0; i < m_numVertices; ++i)
{
EdgeNode* ptmp = m_VertexArray[i].point;
while (ptmp != nullptr)
{
m_VertexArray[i].point = ptmp->next;
delete ptmp;
ptmp = m_VertexArray[i].point;
} //end while
m_VertexArray[i].point = nullptr;
} //end for i
}
public:
//插入顶点
bool InsertVertex(const T& tmpv)
{
if (m_numVertices >= MaxVertices_size) //顶点空间已满
{
cout <<"顶点空间已满"<< endl;
return false;
}
if (GetVertexIdx(tmpv) != -1) //该顶点已经存在
{
cout <<"顶点 "<< tmpv <<" 已经存在!"<< endl;
return false;
}
m_VertexArray[m_numVertices].data = tmpv;
m_VertexArray[m_numVertices].point = nullptr;
m_numVertices++;
return true;
}
//插入边
bool InsertEdge(const T& tmpv1, const T& tmpv2,int weight) //在tmpv1和tmpv2两个顶点之间插入一条边
{
int idx1 = GetVertexIdx(tmpv1);
int idx2 = GetVertexIdx(tmpv2);
if (idx1 == -1 || idx2 == -1) //某个顶点不存在,不可以插入边
return false;
//判断是否边重复
EdgeNode* ptmp = m_VertexArray[idx1].point;
while (ptmp != nullptr)
{
if (ptmp->curridx == idx2)
return false; //边重复
ptmp = ptmp->next;
}
//可以正常插入
ptmp = new EdgeNode;
ptmp->curridx = idx2;
ptmp->weight = weight;
ptmp->next = m_VertexArray[idx1].point; //为简化编码和提升代码执行效率,采用头插法将边节点插入到单链表的最前面
m_VertexArray[idx1].point = ptmp;
m_VertexArray[idx1].outdegree++; //开始顶点出度数增加
m_VertexArray[idx2].indegree++; //终止顶点入度数增加
m_numEdges++; //边数量增加1
return true;
}
void DispGraph() //显示图信息
{
for (int i = 0; i < m_numVertices; ++i)
{
cout << i <<" 入度/出度("<< m_VertexArray[i].indegree <<"/"<< m_VertexArray[i].outdegree <<")"<<""<< m_VertexArray[i].data <<":-->"; //输出顶点下标和顶点数据
EdgeNode* ptmp = m_VertexArray[i].point;
while (ptmp != nullptr)
{
cout << ptmp->curridx <<"(权值:"<< ptmp->weight <<")-->"; //输出顶点相关的边索引(编号)
ptmp = ptmp->next;
}
cout <<"nullptr"<< endl; //显示指向nullptr并换行
} //end for
cout <<"图中有顶点"<< m_numVertices <<"个,边"<< m_numEdges <<"条!"<< endl;
}
//拓扑排序算法
bool TopologicalSort(int *pPopResult, int* pve)
{
int* pInVexDegree = new int[m_numVertices]; //分配空间记录顶点入度
memset(pInVexDegree, 0, sizeof(int) * m_numVertices); //清0
//顶点的入度值先拿过来
for (int i = 0; i < m_numVertices; ++i)
{
pInVexDegree[i] = m_VertexArray[i].indegree;
} //end for
//将入度为0的顶点先入栈
std::stack<int> tempstack; //#include <stack>
for (int i = 0; i < m_numVertices; ++i)
{
if (pInVexDegree[i] == 0)
{
tempstack.push(i);
}
} //end for
int iOutputVexcount = 0; //输出的顶点数量统计
//栈不为空则循环
while (tempstack.empty() == false)
{
//出栈
static int sign = 0;
if (sign == 0)
{
sign = 1;
cout <<"拓扑排序的结果为: ";
}
int topidx = tempstack.top(); //获取栈顶元素
cout << m_VertexArray[topidx].data <<""; //输出没有前趋的顶点
pPopResult[iOutputVexcount] = topidx; //记录出栈的元素顺序
iOutputVexcount++; //输出的拓扑顶点数量统计
tempstack.pop(); //删除栈顶元素
//要将topidx对应顶点的各个邻接点入度减1,所以要先找到第一条边
EdgeNode* pEdgenode = m_VertexArray[topidx].point;
while (pEdgenode != nullptr)
{
int tmpidx = pEdgenode->curridx;
if (pInVexDegree[tmpidx] != 0) //入度已经为0的顶点,不理会
{
pInVexDegree[tmpidx]--; //入度值减1
if (pInVexDegree[tmpidx] == 0)//入度为0的点入栈
tempstack.push(tmpidx);
}
//顺带计算事件的最早发生时间ve供后续CriticalPath计算关键路径使用
if (pve[tmpidx] < (pve[topidx] + pEdgenode->weight))
{
pve[tmpidx] = pve[topidx] + pEdgenode->weight;
}
pEdgenode = pEdgenode->next;
} //end while
} //end while
cout << endl; //换行
delete[] pInVexDegree;
if (iOutputVexcount != m_numVertices) //拓扑排序失败
{
cout <<"输出顶点数量:"<< iOutputVexcount <<",而图中实际顶点数量:"<< m_numVertices <<",说明图中有环,没办法输出所有顶点序列(非AOV网,拓扑排序错误)"<< endl;
return false;
}
return true;
}
//求关键路径
bool CriticalPath()
{
//在AOE网中只有一个入度为0的顶点,称为开始顶点,也只有一个出度为0的顶点,称为结束顶点
int iStartVerIdx = -1;
int iEndVerIdx = -1;
for (int i = 0; i < m_numVertices; ++i)
{
if (m_VertexArray[i].indegree == 0)
{
if (iStartVerIdx != -1)
{
cout <<"图中发现超过1个入度为0的节点,非法AOE网,不能求关键路径"<< endl;
return false;
}
iStartVerIdx = i;
} //end if
if (m_VertexArray[i].outdegree == 0)
{
if (iEndVerIdx != -1)
{
cout <<"图中发现超过1个出度为0的节点,非法AOE网,不能求关键路径"<< endl;
return false;
}
iEndVerIdx = i;
}
} //end for i
//(1)事件的最早发生时间ve分配内存准备开始计算:
int* pve = new int[m_numVertices];
memset(pve, 0, sizeof(int) * m_numVertices); //清0
//这个用来计算后续的vl用的
int * pPopResult = new int[m_numVertices];
memset(pPopResult, 0, sizeof(int) * m_numVertices);
//通过拓扑排序能够得到ve值(当然不通过拓扑排序而是单独计算ve值也可以):
if (TopologicalSort(pPopResult,pve) == false)
{
//内存不要忘记释放
delete[] pve;
delete[] pPopResult;
return false; //图中有环,直接返回
}
//拓扑排序可能的结果为: A B C E G D F H I
//pve结果应该为:0,6,4,5,7,7,16,14,18
//pPopResult的结果应该为:0,1,2,4,6,3,5,7,8
//(2)事件的最迟发生时间vl计算,注意vl值是从后向前求的:
int* pvl = new int[m_numVertices];
memset(pvl, 0, sizeof(int) * m_numVertices);
int toppos = m_numVertices - 1; //栈顶位置=9-1=8
int vexIdx = pPopResult[toppos]; //栈顶位置所代表的顶点的下标值
toppos--;
for (int i = 0; i < m_numVertices; ++i)
{
//初始化vl值,vl值一般都比最大的ve值(pve[idxTop])小,所以把最大ve值先给vl没问题,后续要进行min判断
pvl[i] = pve[vexIdx]; //18
} //end for
while (toppos >= 0) //栈里有数据
{
int fromVexIdx = pPopResult[toppos]; //7:出栈
toppos--;
EdgeNode* pTmpEdge = m_VertexArray[fromVexIdx].point; //下标7所代表的顶点为H,这里拿到H指向的第一条边
while (pTmpEdge != nullptr) //遍历顶点H指向的其他边
{
int toVexIdx = pTmpEdge->curridx; //8
if (pvl[fromVexIdx] > (pvl[toVexIdx] - pTmpEdge->weight))
pvl[fromVexIdx] = pvl[toVexIdx] - pTmpEdge->weight;
pTmpEdge = pTmpEdge->next;
} //end while (pTmpEdge != nullptr)
} //end while(toppos >= 0)
//pvl结果应该为: 0 6 6 8 7 10 16 14 18
//(3)活动的最早开始时间ee计算,该值需要通过ve求得。
//(4)活动的最晚开始时间el计算,该值需要通过vl求得。
//这里不用分配内存并进行计算,只需要求得ee和el临时值,比较他们是否相等就可以得到关键路径了
int tmpee, tmpel;
cout <<"关键路径如下:"<< endl;
for (int fromVexIdx = 0; fromVexIdx < m_numVertices; ++fromVexIdx) //遍历所有顶点
{
EdgeNode* pTmpEdge = m_VertexArray[fromVexIdx].point; //该顶点指向的边信息
while (pTmpEdge != nullptr)
{
int toVexIdx = pTmpEdge->curridx;
int toWeight = pTmpEdge->weight;
tmpee = pve[fromVexIdx]; //活动最早开始时间
tmpel = pvl[toVexIdx] - toWeight; //活动最晚开始时间
//活动最早开始时间和活动最晚开始时间相等,这属于关键路径上的活动
if (tmpee == tmpel)
{
//用“<顶点1,顶点2>(权值=?)”形式表示顶点之间的弧
//结果形如:<A,B>(权值=6) <B,E>(权值=1) <E,H>(权值=7) <E,G>(权值=9) <G,I>(权值=2) <H,I>(权值=4)
cout <<"<"<< m_VertexArray[fromVexIdx].data <<","<< m_VertexArray[toVexIdx].data <<">(权值="<< toWeight <<") ";
}
pTmpEdge = pTmpEdge->next;
}//end while
}//end for
//释放内存
delete[] pve;
delete[] pvl;
delete[] pPopResult;
return true;
}
private:
//获取顶点下标
int GetVertexIdx(const T& tmpv)
{
for (int i = 0; i < m_numVertices; ++i)
{
if (m_VertexArray[i].data == tmpv)
return i;
}
return -1; //不存在的顶点
}
private:
int m_numVertices; //当前顶点数量
int m_numEdges; //边数量
VertexNode<T> m_VertexArray[MaxVertices_size]; //顶点数组
};
|
在main主函数中加入如下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| GraphLink<char> gm;
gm.InsertVertex('A');
gm.InsertVertex('B');
gm.InsertVertex('C');
gm.InsertVertex('D');
gm.InsertVertex('E');
gm.InsertVertex('F');
gm.InsertVertex('G');
gm.InsertVertex('H');
gm.InsertVertex('I');
//向图中插入边
gm.InsertEdge('A', 'B', 6);
gm.InsertEdge('A', 'C', 4);
gm.InsertEdge('A', 'D', 5);
gm.InsertEdge('B', 'E', 1);
gm.InsertEdge('C', 'E', 1);
gm.InsertEdge('D', 'F', 2);
gm.InsertEdge('E', 'G', 9);
gm.InsertEdge('E', 'H', 7);
gm.InsertEdge('F', 'H', 4);
gm.InsertEdge('G', 'I', 2);
gm.InsertEdge('H', 'I', 4);
gm.DispGraph();
gm.CriticalPath();
|
执行结果如下:

最终得到的AOE网关键路径如图8所示:
从整个关键路径算法CriticalPath的实现来看,因为调用了拓扑排序算法,拓扑排序算法的时间复杂度是O(|V|+|E|),双while嵌套计算事件的最迟发生时间vl的时间复杂度也是O(|V|+|E|),用for嵌套while循环获取关键路径这段代码的时间复杂度还是O(|V|+|E|)。所以,上述关键路径算法的时间复杂度是O(|V|+|E|)。
一般来说,求得事件的最早发生时间ve和事件的最迟发生时间vl是需要借助拓扑排序来进行以保证各个顶点相关值的求解顺序的。在翻阅和这节课相关的资料和实现代码中,我遇到过不通过拓扑排序直接求得ve和vl值,从而再进一步求得活动的最早开始时间ee和活动的最晚开始时间el并最终求得关键路径的情况。但是经过对源码的分析和测试后,我认为实现有问题:在测试代码中,只需要把顶点A的创建顺序从最前面放到最后面,也就是在创建图中顶点时,按照下面的顺序创建各个顶点。
1
2
3
4
5
6
7
8
9
| gm.InsertVertex('B');
gm.InsertVertex('C');
gm.InsertVertex('D');
gm.InsertVertex('E');
gm.InsertVertex('F');
gm.InsertVertex('G');
gm.InsertVertex('H');
gm.InsertVertex('I');
gm.InsertVertex('A');
|
按这样的顺序创建顶点后,其实整个图并没有发生什么改变。然后我们输出并判断计算出的ve值是否依旧正确,如果不正确,则说明实现关键路径的算法代码有问题。
小结
这节课我们学习了通过关键路径估算完成工程需要的最短时间,从而想办法提高生产效率的问题。
我们首先引入了AOE网的概念和性质,以做一盘番茄炒蛋菜为例,估算了做一盘番茄炒蛋菜所需要的最短时间,为使估算过程顺利进行,我们也引入了关键路径和关键活动这两个重要概念。
为了更好地编程实现关键路径求解问题,我们引入了一些与关键活动有关的概念以及他们的计算,这些概念包括:
- 事件vk的最早发生时间ve[k]
- 事件vk的最迟发生时间vl[k]
- 活动ai的最早开始时间ee[i]
- 活动ai的最晚开始时间el[i]
有了这些概念作为铺垫,我们才能去实现求AOE网中关键路径的代码编写工作。代码实现虽然相对烦琐,但整个难度并不大。这里需要提醒你的是,只有带权有向无环图才能求关键路径。最后,我们需要知道,通过关键路径算法可以找出关键活动,如果不按期完成会影响整个工程进度的活动。
课后思考
请你仿照本节所讲述的做一盘番茄炒蛋菜的工程来规划一个新的工程,绘制出该工程所代表的AOE网并求出该AOE网对应的关键路径信息。
欢迎你在留言区分享自己的思考。如果觉得有所收获,也可以把课程分享给更多的同学一起学习进步。我们下节课见!

















