35、冒泡排序：大数下沉，小数上浮

你好，我是王健伟。

前面我带你学习了插入类排序中的直接插入排序和希尔排序，这次，我们讲解另一类排序——交换类排序。

所谓交换类排序，就是根据序列中两个关键字的比较结果，来决定是否要交换这两个关键字对应的记录在序列中的位置。

交换类排序主要包括冒泡排序和快速排序，这在前面已经提到过。这节课，我先带你看一看冒泡排序。

冒泡排序基本概念

冒泡排序的英文名称是Bubble Sort，也叫起泡排序。

按照从小到大排序来说，它的基本思想是在有n个元素的序列中，先将第一个记录的关键字和第二个记录的关键字进行比较，也就是两两比较相邻记录关键字，如果第一个记录的关键字大于第二个记录的关键字，则交换这两个记录。接着，比较第二个记录的关键字和第三个记录的关键字，如果第二个记录的关键字大于第三个记录的关键字，则交换这两个记录。依次类推，直到第n-1个记录和第n个记录比较完为止。

上述这些过程叫第一趟冒泡排序。这样做的结果就是将关键字最大的记录放到了最后一个记录位置上。显然，对于数组{16,1,45,23,99,2,18,67,42,10}，第一趟冒泡排序后，结果为{1,16,23,45,2,18,67,42,10,99}。如图1所示：

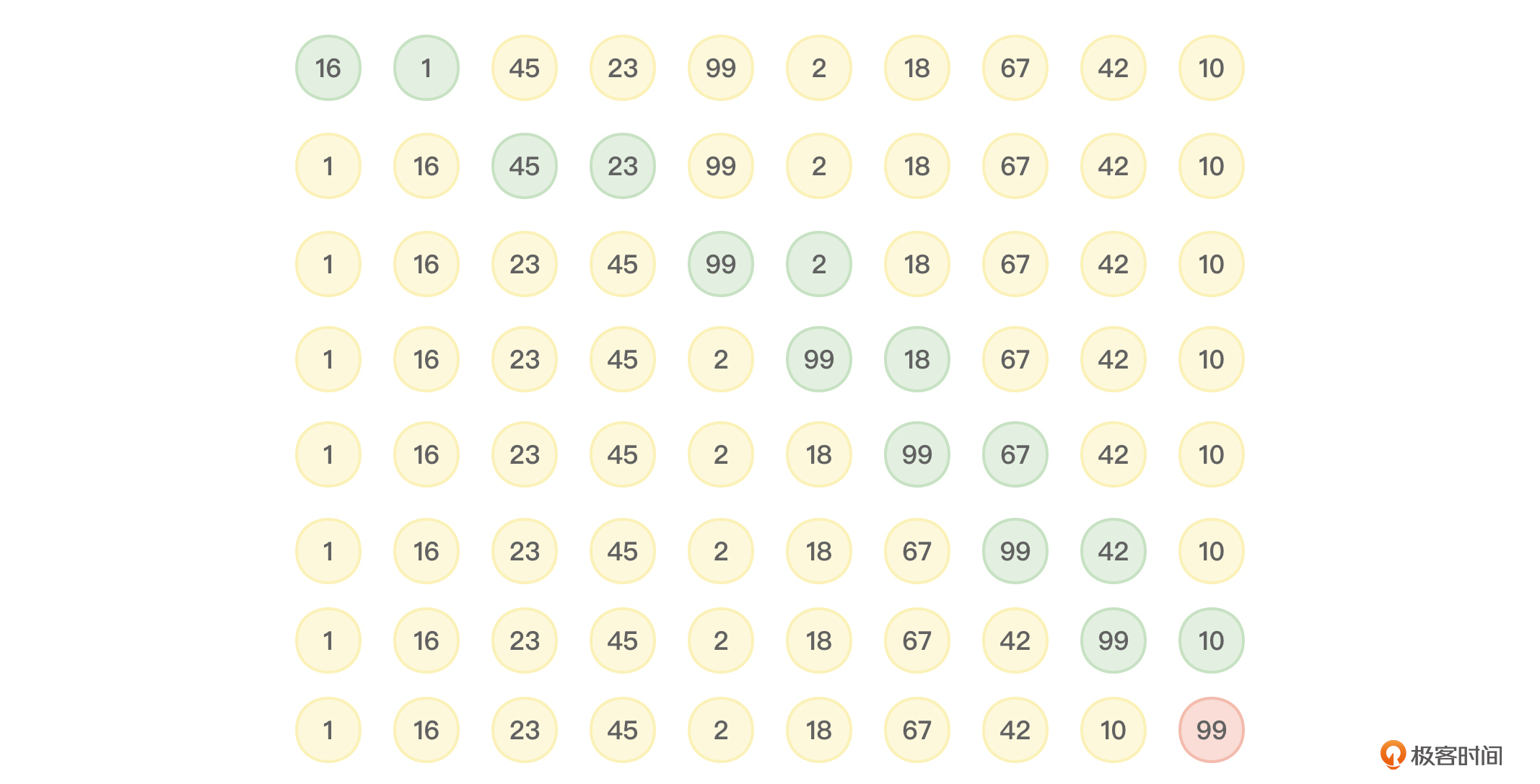
之所以称为冒泡排序，是因为大的数据往最下面（后面）沉，小的数据自然就会向上冒，这个过程就好像气泡在水中上浮的过程，所以叫做冒泡排序。

接着要开始第二趟冒泡排序了。但因为最后一个记录已经是最大值，因此第二趟冒泡排序只需要两两比较前n-1个元素，这样就会把第二大的记录放到倒数第二个记录位置上。显然，接着第一趟冒泡排序的结果，第二趟冒泡排序的结果为{1,16,23,2,18,45,42,10,67,99}。如图2所示：

接着开始第三趟、第四趟……冒泡排序，当在一趟排序中没有进行过记录交换的操作时，就可以认为冒泡排序结束了。具体实现我会在下面的冒泡排序算法的改进代码中进行展示。

实现代码

冒泡排序的代码编写有很多种方法，比如有的方法会从序列中的最后两条记录开始比较，把关键字最小的记录不断向最前面移动。

这里我选择的编码方式还是按照本节最开始描述的冒泡排序基本思想来实现，下面是具体代码。

//冒泡排序（从小到大）
template<typename T>
void BubbleSort(T myarray[], int length)
{
	if (length <= 1) //不超过1个元素的数组，没必要排序
		return;
	
	//外层循环只控制排序的趟数
	for (int i = 0; i < length - 1; ++i)
	{
		//内层循环控制元素的大小比较和交换位置
		for (int j = 0; j < length - i - 1; ++j) //每趟比较的次数都会减少
		{
			if (myarray[j] > myarray[j + 1])  //前面的数据如果比后面的数据大
			{
				//交换元素位置
				T temp = myarray[j + 1];
				myarray[j + 1] = myarray[j];
				myarray[j] = temp;
			}
		} //end for j
		
		//每走一趟显示一下结果
		cout <<"第"<< i+1 <<"趟冒泡排序结果为： ";
		for (int i = 0; i < length; ++i) cout << myarray[i] <<"";
		cout << endl;
	} //end for i
	return;
}

在main主函数中，加入下面的测试代码。

int arr[] = {16,1,45,23,99,2,18,67,42,10};
int length = sizeof(arr) / sizeof(arr[0]);   //数组中元素个数
BubbleSort(arr, length);//对数组元素进行冒泡排序

cout <<"冒泡排序结果为：";
for (int i = 0; i < length; ++i)
{
	cout << arr[i] <<" ";
}
cout << endl; //换行

执行结果如下：

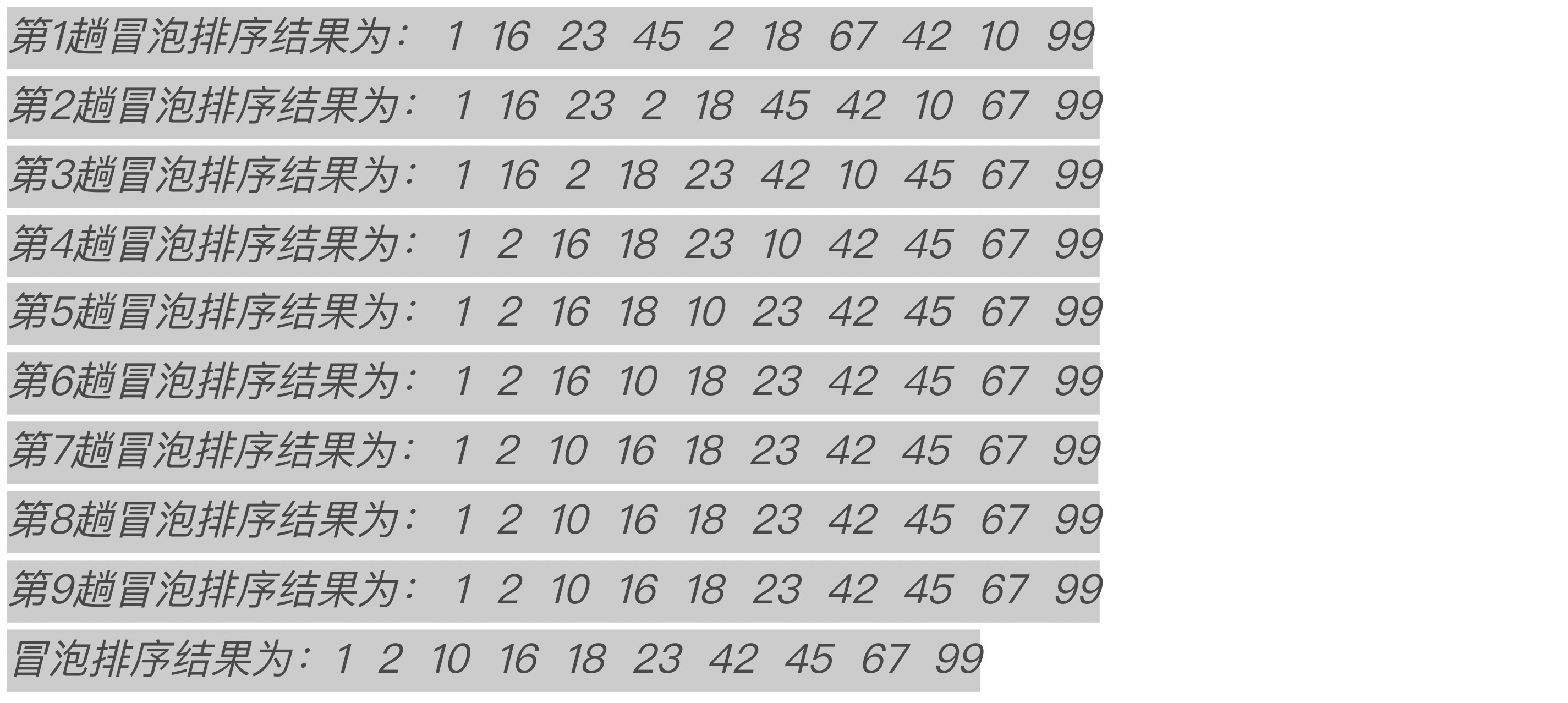
从结果可以看到，第7、8、9趟冒泡排序的结果相同，这意味着第8和第9趟排序是没有必要的，也就是这个算法可以提前结束。换句话说。冒泡排序的结束条件应该是“在一趟排序中没有进行过记录交换的操作”。

所以，可以对上述冒泡排序算法BubbleSort进行改进，下面是改进后的代码。

//冒泡排序（从小到大）
template<typename T>
void BubbleSort(T myarray[], int length)
{
	if (length <= 1) //不超过1个元素的数组，没必要排序
		return;
	
	//外层循环只控制排序的趟数
	for (int i = 0; i < length - 1; ++i)
	{
		bool cgflag=false;//表本趟冒泡排序是否发生过记录交换，false：无；true：有
		//内层循环控制元素的大小比较和交换位置
		for (int j = 0; j < length - i - 1; ++j) //每趟比较的次数都会减少
		{
			if (myarray[j] > myarray[j + 1])  //前面的数据如果比后面的数据大
			{
				//交换元素位置
				T temp = myarray[j + 1];
				myarray[j + 1] = myarray[j];
				myarray[j] = temp;
				
				cgflag = true; //标记本趟冒泡排序发生过记录交换(可能1次或者多次)
			}
		} //end for j
		if (cgflag == false) //本趟冒泡排序没有发生过记录交换，表示整个冒泡排序结束
			break; 
		
		//每走一趟显示一下结果
		cout <<"第"<< i+1 <<"趟冒泡排序结果为： ";
		for (int i = 0; i < length; ++i) cout << myarray[i] <<"";
		cout << endl;
	} //end for i
	return;
}

main主函数中代码不变，执行结果如下：

分析代码和结果可以看到，当进行第8趟冒泡排序后，因为没有发生记录交换，所以直接跳出外循环从而结束整个冒泡排序的过程。

从代码中可以看到，冒泡排序实现代码比较简单。空间复杂度为O(1)。

在时间复杂度方面，对于具有n个元素的数组，在最好的情况下，即数组中元素已经是排好序的情况下，则只需要一趟排序并且这趟排序只需要进行n-1次比较次数且不需要做任何数据交换，所以最好情况时间复杂度为O(n)。

在最坏情况下，即数组中元素正好是逆序排列的情况下，此时需要进行n-1趟排序，比较次数和记录交换次数都是1+2+3+……+(n-1)= $\frac{n(n-1)}{2}$次，即最坏情况时间复杂度为O($n^{2}$)。

平均情况时间复杂度的分析要结合一些概率论知识，这里就不详细说明，结论也是O($n^{2}$)。此外，从实现代码中不难看到，即使遇到了关键字相同的两条记录，这两条记录的相对顺序也不会发生改变，所以此排序算法是稳定的。

小结

本节课我带你学习了交换类排序中的冒泡排序。

交换类排序是根据序列中两个关键字的比较结果来决定是否要交换这两个关键字所对应的记录在序列中的位置。而冒泡排序是将大数据下沉，使小数据不断上冒来进行数据排序的算法。

冒泡排序会进行多趟排序，每趟排序都会把当前参与排序的数字中的最大数字下沉到最后，当然，不能影响已经在最后面的排好序的数字。

虽然冒泡排序算法的编码方式各种各样，但我带你实现了的这种冒泡排序算法是典型的严格遵照冒泡排序算法的定义来实现的。这里要注意，不用一开始就想着优化自己的代码，从最基础的思想入手，反而会更加脚踏实地。之后，我也依据实际情况对该冒泡排序算法进行了改进以进一步提升其执行性能。

冒泡排序算法的实现比较简单好理解，是一种稳定的排序算法。该算法的平均情况时间复杂度为O($n^{2}$)，当待排序数据量比较大的情况下，排序速度会减慢，此时就应该采用其他排序方法了。下节课，我们就来说说快速排序算法。

思考题

两种冒泡排序算法，第一种是按照从小到大排序，第二种是按照从大到小排序，这两种排序算法的实现过程是否相同？
有没有什么办法能够优化冒泡排序算法，使其时间复杂度进一步减小呢？

欢迎在留言区和我分享你的思考。如果觉得有所收获，也可以把课程分享给更多的朋友一起学习进步。我们下节课见！