你好,我是王健伟。
在选择类排序中,除了我们以往学习过的简单选择排序和堆排序之外,比较重点的还有树形选择排序,因为这种排序在面试中也偶有出现,所以这节课我们也来讲一讲。
基本概念与算法描述
树形选择排序又叫锦标赛排序(Tournament Sort),是一种按照锦标赛的思想进行选择排序的方法。属于对简单选择排序的一种改进。
我们尝试描述一下树形选择排序算法:对n个记录的关键字进行两两比较。然后在其中 ⌈$\frac{n}{2}$⌉ 个较小者中再进行两两比较,如此重复,直到选出最小关键字(按从小到大排序)为止。
以数组 { 16,1,45,23,99,2,18,67,42,10 } 为例,参考图1。
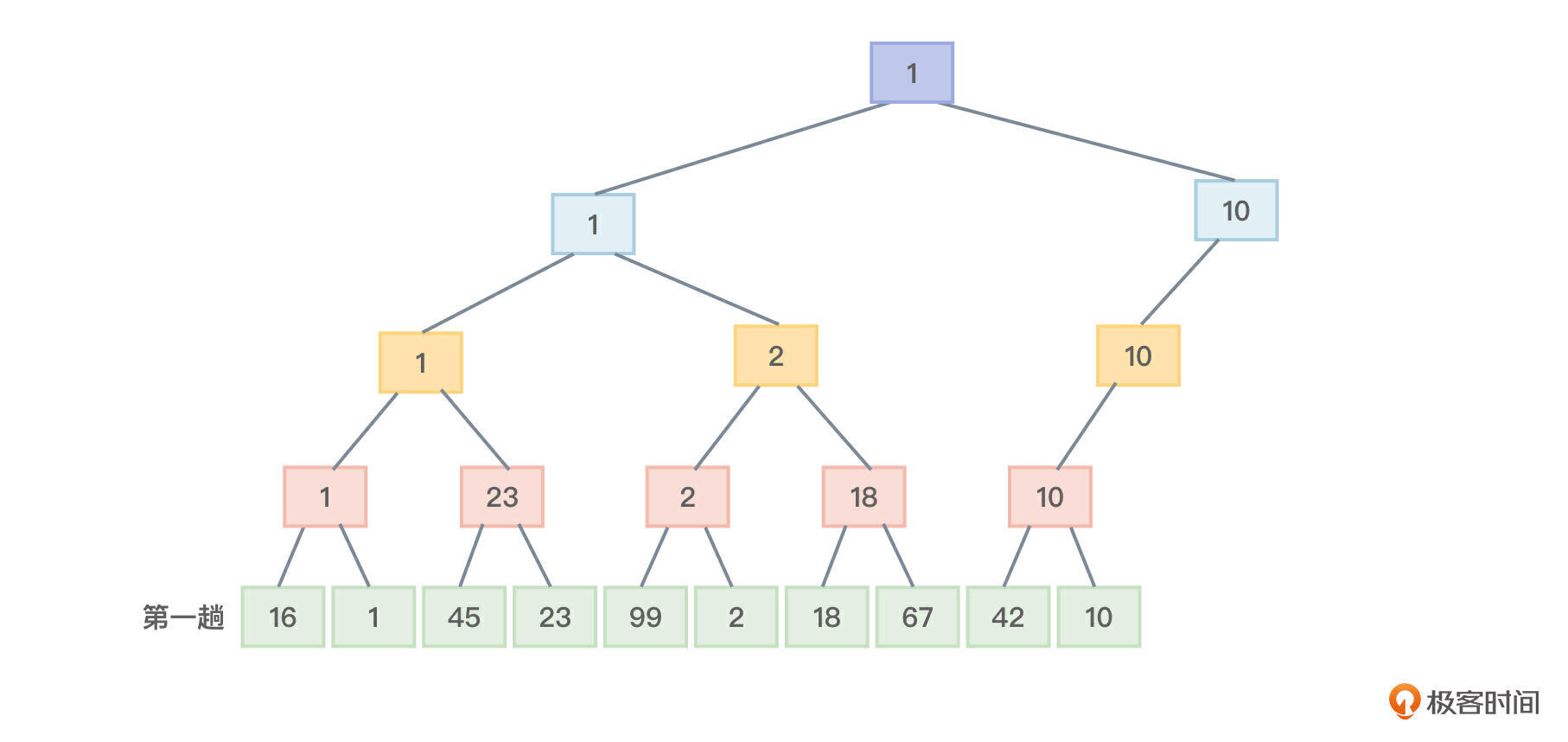
图1从下向上观察,这是第一趟排序,目的是从所有数组中选出值最小的元素。我们尝试描述下具体的操作步骤。
- 开始两两比较,于是元素16和1比较选择1,元素45和23比较选择23,元素99和2比较选择2,18和67比较选择18,42和10比较选择10。
- 现在,选择出的元素1、23、2、18、10又进行两两比较,元素1和23比较选择1,元素2和18比较选择2,元素10没有比较的对象直接被选择。
- 现在,选择出的元素1、2、10又进行两两比较,元素1和2比较选择1,元素10没有比较的对象直接被选择。
- 现在,选择出的元素1、10又进行比较,选择1。最终这个1也是树形结构的树根,找个地方保存本趟排序的最小元素1。
接着,在树叶中把第一趟已经选择出的元素1标记为一个最大值 ∞(这表示元素1不可能在比较中被再次选中了),然后进行第二趟排序,如图2所示。
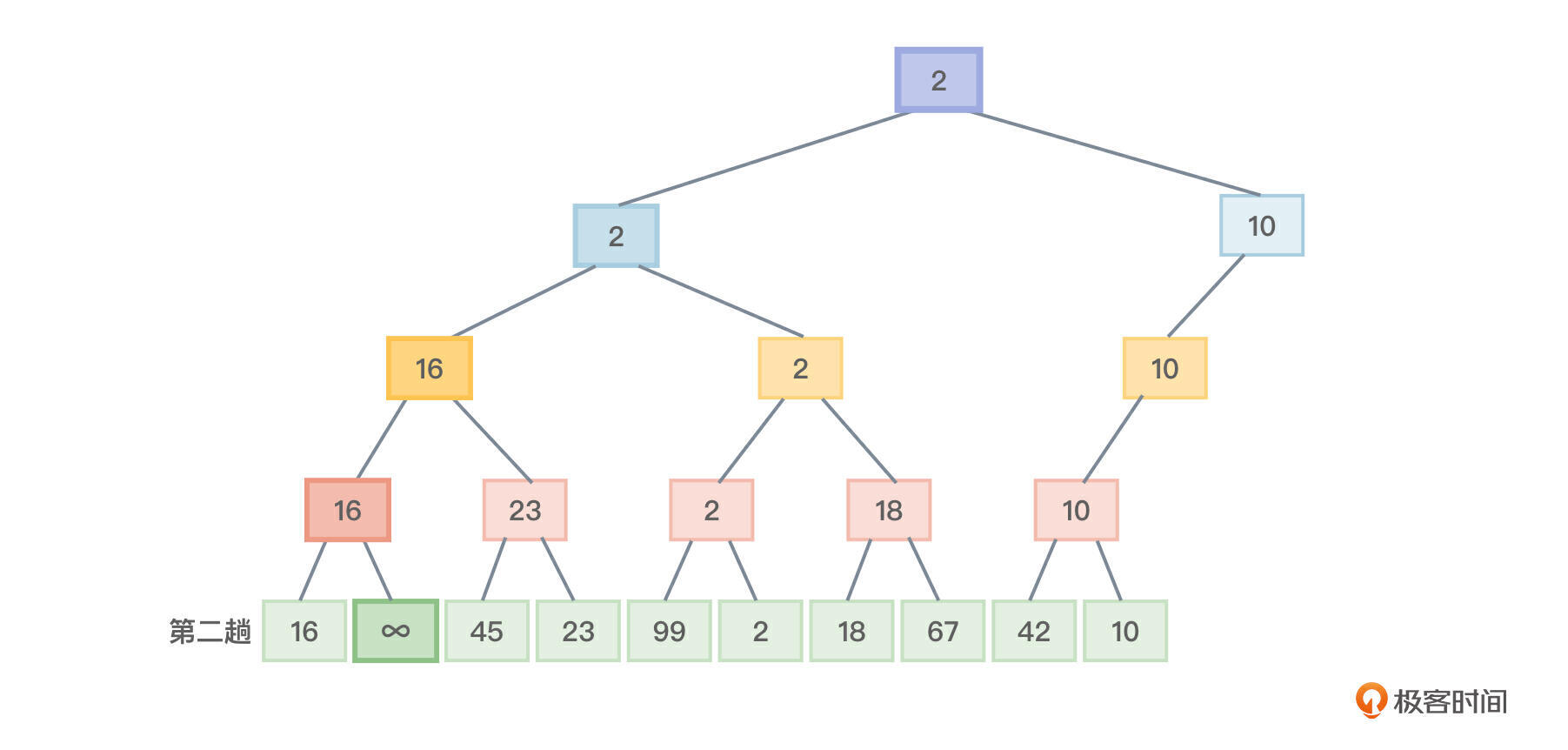
图2还是从下向上观察,这是第二趟排序,前面挑选出的最小值1已经找了个地方保存,这里直接把1的值修改为一个最大值∞,这样,对节点进行两两比较时,标记为最大值的节点就不可能被选中。第二趟排序需要进行什么比较呢?
- 开始两两比较,元素16和最大值比较,选择元素16。元素45和23、99和2、18和67、42和10就不需要再次比较(因为第一趟排序比较过了)。
- 现在,选择出的元素16和23比较,选择元素16。元素2和18,元素10同样因为第一趟比较过,不需要再次比较。
- 现在,选择出的元素16和2比较,元素10同样因为第一趟比较过,不需要再次比较。
- 现在,选择出的元素2、10进行比较,选择2。最终这个2也是树形结构的树根,找个地方保存本趟排序的最小元素2。
然后继续把第二趟中已经选择出的元素2标记为一个最大值,就可以开始第三趟排序,这里就不赘述了。
所以可以看到,经过一次(第一趟)的完全比较后,从第二趟开始就不再需要完全的两两比较,这样就达到了节省时间提高效率的目的,这就是树形选择排序相较于简单选择排序一个重大的改进之处。但是也应该看到,树形选择排序需要通过构造出二叉树这种树形结构来辅助排序,所以还需要辅助存储空间。
上述图1和图2意在阐述树形选择排序理论,理论上来说树形选择排序并不复杂。但若通过代码实现,则是需要构建一棵完全二叉树来实现对数据排序的。换句话说,图1和图2绘制得比较简单,很多额外的节点并没有绘制出来。
回忆一下二叉树的性质5——具有n(n>0)个节点的完全二叉树的高度为 ⌈$log_{2}^{n+1}$⌉ 或者 ⌊$log_{2}^{n}$⌋ +1。同时,你也需要知道,含有n个叶子节点的完全二叉树的高度是 ⌈$log_{2}^{n}$⌉ +1。以这个理论为指导(为了能够正确编写出代码),绘制一下更详细的树形选择排序示意图。依旧以数组 { 16,1,45,23,99,2,18,67,42,10 } 举例来解释树形选择排序。
- 把该数组中的所有元素都看成是完全二叉树的叶子,根据“含有n个叶子节点的完全二叉树的高度是 ⌈$log_{2}^{n}$⌉ +1”,树形选择排序所要创建的这棵完全二叉树高度应该是5。
- 第一趟,两两比较,找到最小值保存到根节点中,如图3所示。
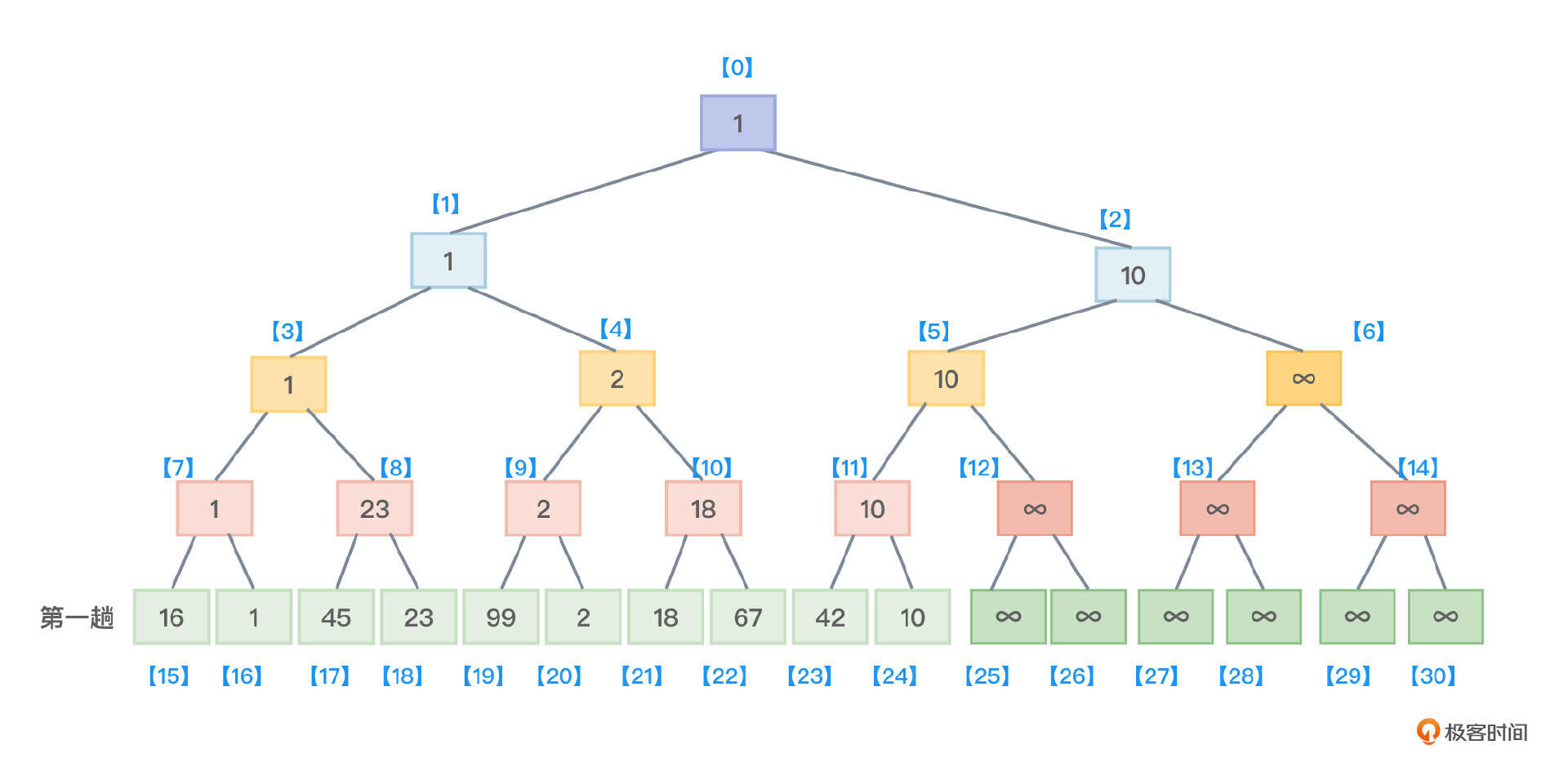
- 接着,沿着根节点向叶子节点找,找到了最小值1所在的叶子节点,把该叶子节点的值从原来保存的1修改为最大值 ∞,如图4所示。
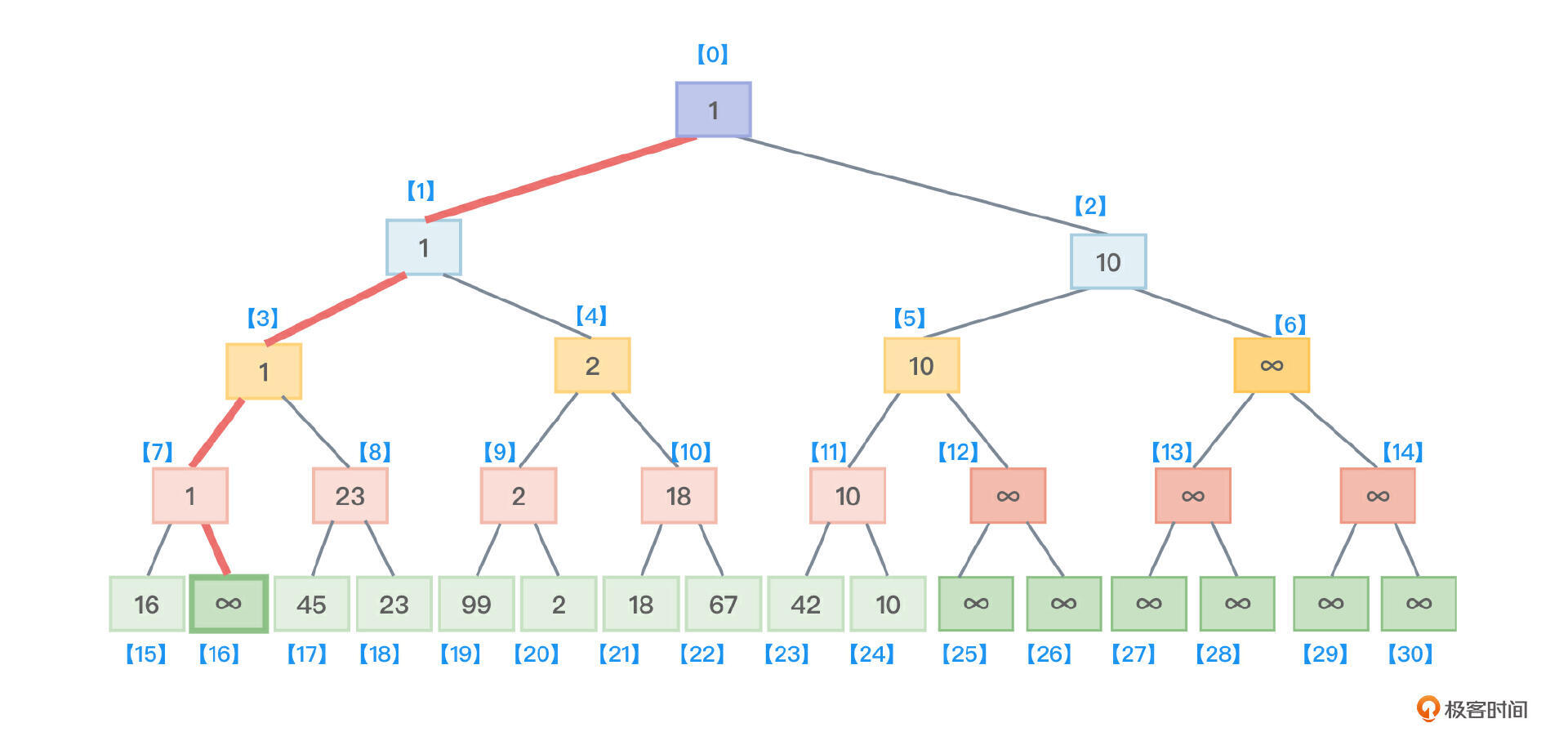
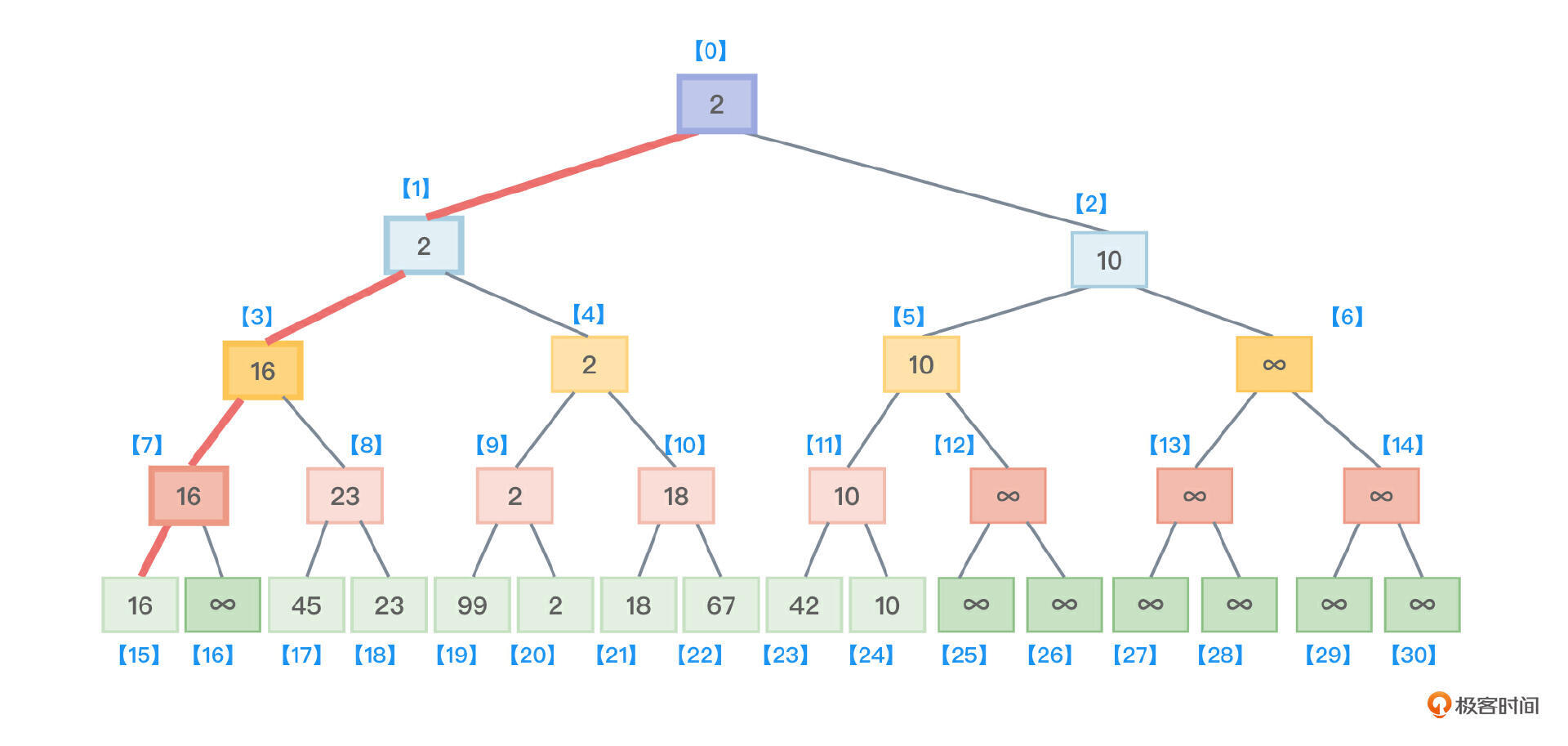
- 接着要开始第二趟比较了,第二趟比较时叶子节点之间不再需要两两比较,只需要16和∞作比较,此时当然是16更小,于是,沿着这个比较路线再前进到树根,就能把当前树中的最小节点找到并保存到根中。如图5所示。
- 接着,沿着根节点向叶子节点找,找到了最小值2所在的叶子节点,把该叶子节点的值从原来保存的2修改为最大值 ∞,如图6所示。
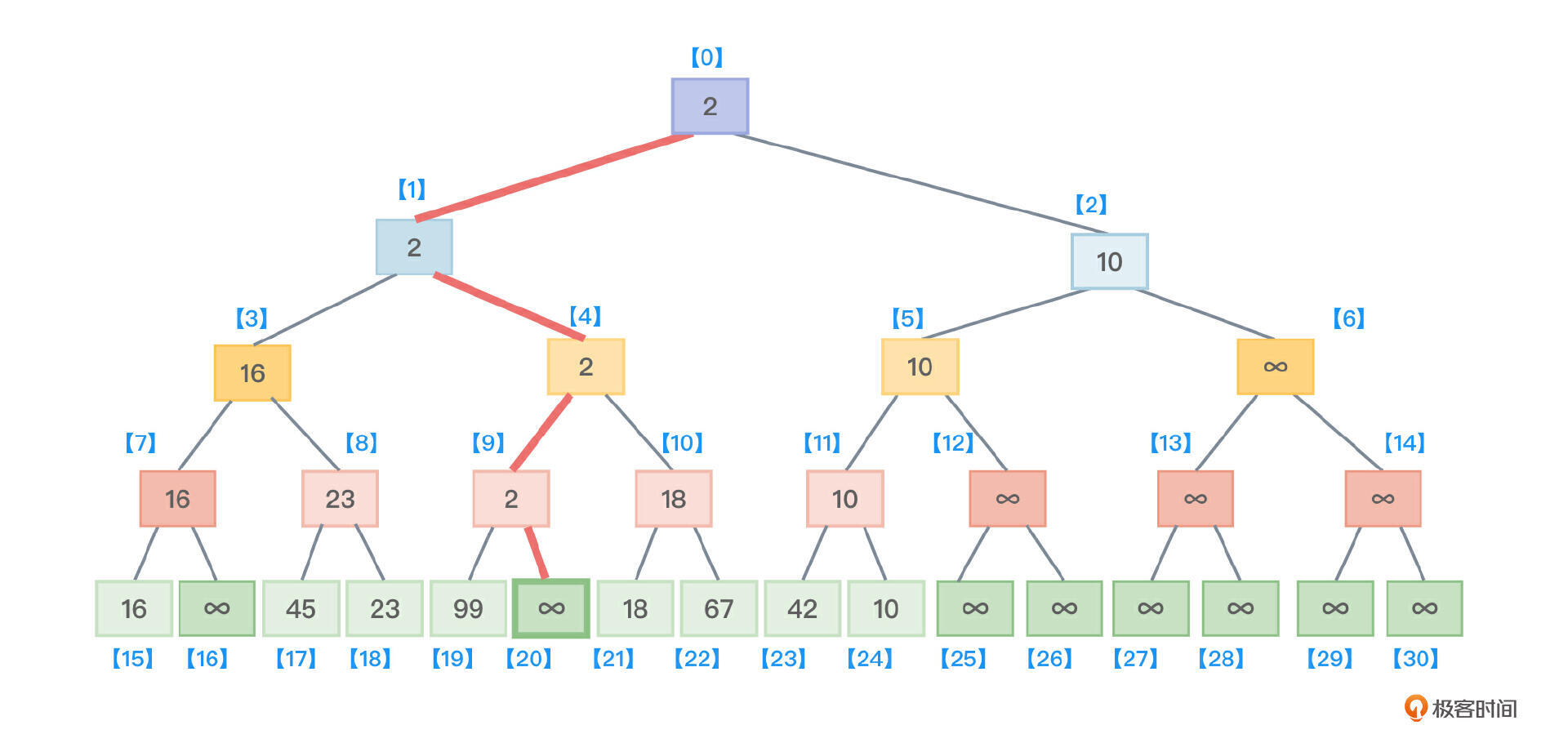
持续上述步骤,就可以把整个数据序列按从小到大的顺序排列好。
实现代码
下面我给出树形选择排序的实现代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
| #define INT_MAX_MY 2147483647//整型能够保存的最大数值,作为标记使用
//树形选择排序(从小到大)
template<typename T>
void TreeSelSort(T myarray[], int length)
{
//ceil是系统函数:ceil(x)函数返回的是大于或等于x的最小整数
int treelvl = (int)ceil(log(length) / log(2)) + 1; //5:完全二叉树高度(含有n个叶子节点的完全二叉树的高度是⌈logn⌉ +1)
//treelvl高的完全二叉树最多有nodecount个节点,如果有nodecount个节点,此时的完全二叉树其实是满二叉树
int nodecount = (int)pow(2, treelvl) - 1; //31:满二叉树是指一棵高度为h,且含有2h-1个节点的二叉树
//treelvl-1 高的完全二叉树最多有nodecount2个节点
int nodecount2 = (int)pow(2, treelvl - 1) - 1; //15
int* pidx = new int[nodecount];//保存节点的下标用的内存
//叶子节点保存元素的下标值(就等于保存了元素的值)
for (int i = 0; i < length; ++i)
{
pidx[nodecount2 + i] = i; //pidx[15] = 0; pidx[16] = 1....;pidx[24] = 9
} //end for
//给多余的叶子节点赋予一个最大值作为标记
for (int i = nodecount2 + length; i < nodecount; ++i) //i=25~30
{
pidx[i] = INT_MAX_MY; //pidx[25] = MAX;pidx[26] = MAX; ......pidx[30] = MAX
}
int tmpnode2 = nodecount2; //15
int tmpnode = nodecount; //31
//现在要开始给非叶子节点赋值了,非叶子节点下标是[0]~[14]
//第一趟排序要给非叶子节点赋值,还要两两进行节点比较,所以要单独处理
while (tmpnode2 != 0)
{
//第一次for执行i值分别为:15、17、19、21、23、25、27、29
//第二次for执行i值分别为:7,9,11,13
//第三次for执行i值分别为:3,5
//第四次for执行i值分别为:1
for (int i = tmpnode2; i < tmpnode; i += 2)
{
//第一次for这个pidx的下标【(i + 1) / 2 - 1】分别是7,8,9,10,11,12,13,14
//第二次for这个pidx的下标【(i + 1) / 2 - 1】分别是3,4,5,6
//第三次for这个pidx的下标【(i + 1) / 2 - 1】分别是1,2
//第四次for这个pidx的下标【(i + 1) / 2 - 1】分别是0
//把两个孩子中小的孩子值给爹
if (pidx[i] != INT_MAX_MY && pidx[i + 1] != INT_MAX_MY) //如果pidx[i]和pidx[i+1]都是正常值,那自然是可以比较
{
if (myarray[pidx[i]] <= myarray[pidx[i + 1]])
{
pidx[(i + 1) / 2 - 1] = pidx[i];
}
else
{
pidx[(i + 1) / 2 - 1] = pidx[i + 1];
}
}
else if( pidx[i] != INT_MAX_MY) //pidx[i]是正常值,因为有上个if在,说明pidx[i + 1]不是正常值
{
pidx[(i + 1) / 2 - 1] = pidx[i];
}
else //走到这里,说明pidx[i + 1]是正常值或者是INT_MAX_MY值
{
pidx[(i + 1) / 2 - 1] = pidx[i + 1];
}
} //end for
tmpnode = tmpnode2; //15,7,3,1
tmpnode2 = (tmpnode2 - 1) / 2; //7,3,1,0
} //end while
T* ptmparray = new T[length]; //临时保存排好序的数据
for (int i = 0; i < length; i++)
{
ptmparray[i] = myarray[pidx[0]]; //将当前最小值赋给ptmparray[i]临时保存
int leafidx = 0;
//沿树根找最小值结点在叶子中的序号
//leafidx = 0,1,3,7,16分别追溯到叶子中的编号
for (int j = 1; j < treelvl; j++)
{
if (pidx[2 * leafidx + 1] == pidx[leafidx])
{
leafidx = 2 * leafidx + 1;
}
else
{
leafidx = 2 * leafidx + 2;
}
} //end for j
//此时的leafidx就是完全二叉树叶子节点中的那个最小值的下标
pidx[leafidx] = INT_MAX_MY; //leafidx = 16。
while (leafidx)
{
//leafidx = 7,3,1,0
leafidx = (leafidx + 1)/2 - 1;//序号为leafidx的结点的双亲结点序号
if (pidx[2 * leafidx + 1] != INT_MAX_MY && pidx[2 * leafidx + 2] != INT_MAX_MY) //如果pidx[i]和pidx[i+1]都是正常值,那自然是可以比较
{
if (myarray[ pidx[2 * leafidx + 1]] <= myarray[pidx[2 * leafidx + 2]])
{
pidx[leafidx] = pidx[2 * leafidx + 1];
}
else
{
pidx[leafidx] = pidx[2 * leafidx + 2];
}
}
else if (pidx[2 * leafidx + 1] != INT_MAX_MY)
{
pidx[leafidx] = pidx[2 * leafidx + 1];
}
else
{
pidx[leafidx] = pidx[2 * leafidx + 2];
}
}//end while
} //end for i
//把数据从ptmparray拷贝回myarray
for (int i = 0; i < length; i++)
{
myarray[i] = ptmparray[i];
} //end for i
//释放内存
delete[] ptmparray;
delete[] pidx;
return;
}
|
在main主函数中,加入测试代码。
1
2
3
4
5
6
7
8
9
| int arr[] = {16,1,45,23,99,2,18,67,42,10};
int length = sizeof(arr) / sizeof(arr[0]); //数组中元素个数
TreeSelSort(arr, length);//对数组元素进行树形选择排序
cout <<"树形选择排序结果为:";
for (int i = 0; i < length; ++i)
{
cout << arr[i] <<"";
}
cout << endl; //换行
|
代码的执行结果如下:

树形选择排序算法因为含有n个叶子节点的完全二叉树的高度是 ⌈$log_{2}^{n}$⌉ +1,除了最小关键字外,每次选择其他最小关键字只需要 ⌈$log_{2}^{n}$⌉ 次比较,因为还有 n-1 个关键字需要进行这个次数的比较,所以可以认为该算法的时间复杂度是 O(n$log_{2}^{n}$)。
对于算法的空间复杂度,在上述实现代码中,是需要一些辅助空间帮忙实现排序的(空间换时间),比如存储完全二叉树节点,还可能需要存储其他一些数据比如临时的排好序的数据。当然,也可以用其他办法,而不是必须用临时空间保存排好序的数据,不过总体来看,树形选择排序的空间复杂度为O(n)。
此外,经过我测试,认为上述算法的实现代码是稳定的。如果你稍微调整一下其实现代码,改为不稳定的也很容易。
小结
这节课我带你一起学习了选择类排序中的树形选择排序。树形选择排序是一种按照锦标赛的思想进行选择排序的方法,属于对简单选择排序的一种改进。它会通过多趟排序来对n个记录的关键字进行两两比较,然后在其中 ⌈$\frac{n}{2}$⌉ 个较小者中再进行两两比较,如此重复,直到选出最小关键字(按从小到大排序)为止。
**树形选择排序的每一趟排序都会减少需要两两比较的元素数量,从而达到了节省时间提高效率的目的,这就是树形选择排序相较于简单选择排序一个重大的改进之处。**但是我们也应该看到,树形选择排序需要通过构造出二叉树这种树形结构来辅助排序,所以还需要辅助存储空间。
这节课我们也详细解释了树形选择排序的概念,通过多个示意图对该排序的算法进行了详尽的描述,也为你提供了完整的实现代码。最后强调一个细节,树形选择排序算法的时间复杂度是 O(n$log_{2}^{n}$),空间复杂度为 O(n),算法是稳定的。
思考题
在这节课的最后,我也给你留了几道复习思考题。
- 请描述用树形选择排序对以下数组进行排序的过程 { 15,6,2,23,8,9,27,12 } 。
- 试比较树形选择排序与堆排序的区别。
欢迎你在留言区和我互动。如果觉得有所收获,也可以把课程分享给更多的朋友一起学习。我们下节课见!






