你好,我是王健伟。
从“链表”毕业之后,我们就要进入“栈”的学习了。作为一种耳熟能详的数据结构,“栈”到底是个什么东西呢?
还记得我们之前提到过的线性表吗?没错,栈仍旧是一种线性表。不过它只能在一端进行插入和删除操作,先入栈的数据只能后出来,而后入栈的数据只能先出来。所以栈具有先进后出或者后进先出的特性。通常来说,我们可以把栈理解为一种受限的线性表。
如果我们把栈比成一个类似木桶这样的容器,栈有两端,把允许进行插入和删除操作的一端称为栈顶(top)也就是桶口,或者称为线性表的表尾,而另一端称为栈底(bottom)也就是桶底,或者称为线性表的表头。不包含任何数据的栈,叫做空栈(空线性表)。
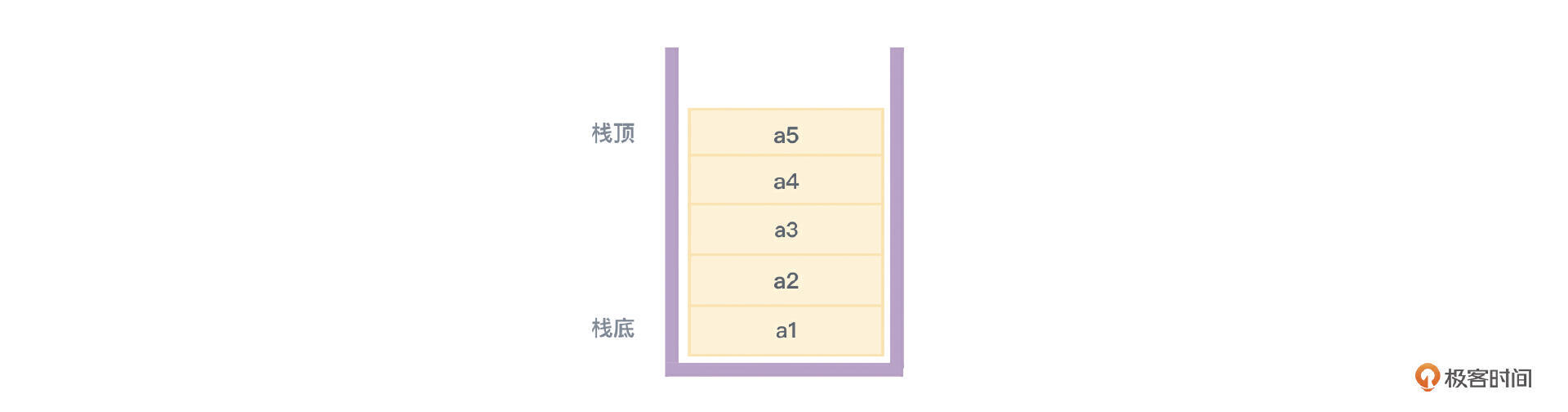
整体结构理清之后,我们再说相关的操作。向栈中插入元素,可以叫做入栈或进栈,从栈中删除元素,就叫出栈。除了能够在表尾插入和删除数据外,对于栈这种数据结构,在任何其他位置插入和删除数据都不应该被允许。你只能提供符合这个规定的操作接口,否则实现的就不是栈了。
栈也被称为后进先出(Last In First Out:LIFO)的线性表,这意味着最后放入到栈里的数据(插入数据)只能最先被从栈中拿出来(删除数据)。
其实,我们生活中满足栈这种后进先出的情形非常多,比如往抽屉里放东西,先放进去的肯定会被堆到最里面,所以只能最后取出,而最后放入的物品往往在最前面或者最上面,所以会被最先取出。
如果用示意图表示用栈存取数据的过程,就会像图1一样:
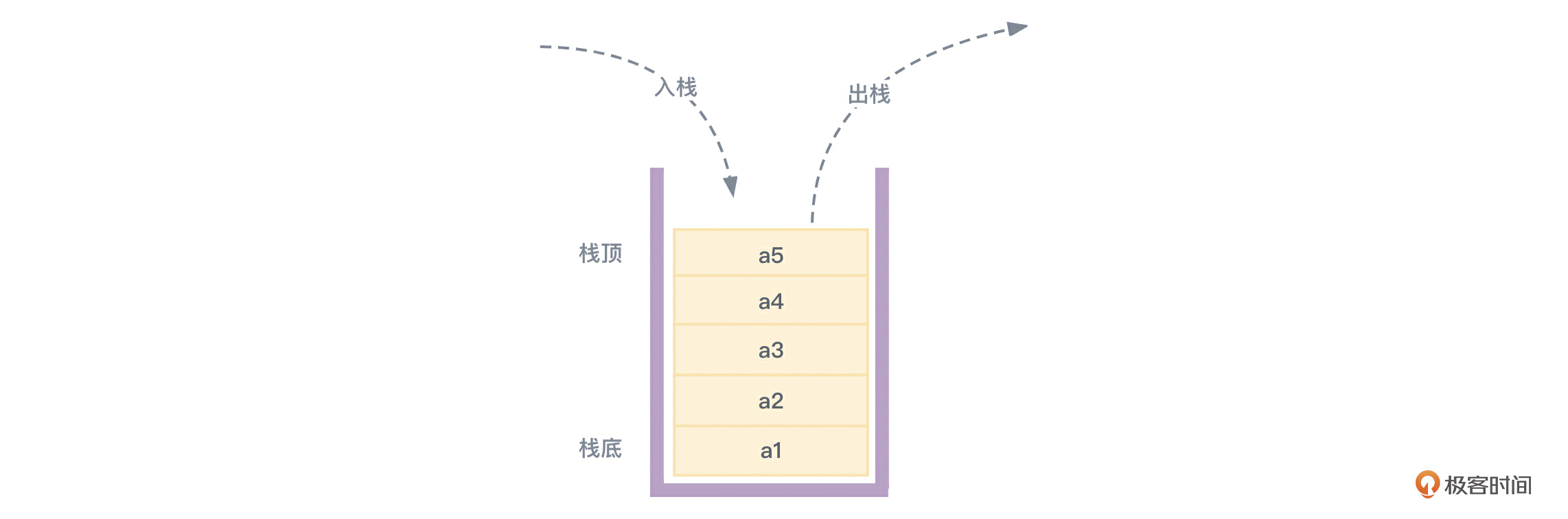
在图1中,如果分别将数据a1、a2、a3、a4、a5存入栈中,那么在将数据出栈的时候,顺序就应该是a5、a4、a3、a2、a1(与入栈顺序正好相反)。
我们刚刚说过,栈是受限的线性表,比如因为只能在栈顶进行元素的插入和删除操作,所以也无法指定插入和删除操作的位置,所以,栈所支持的操作,可以理解为线性表操作的子集,一般包括栈的创建、入栈(增加数据)、出栈(删除数据)、获取栈顶元素(查找数据)、判断栈是否为空或者是否已满等操作。
栈的顺序存储(顺序栈)
所谓顺序栈,就是顺序存储(用一段连续的内存空间依次存储)栈中的数据。前面我们在学习顺序表的时候就提出过2种保存数据的方案同样适合顺序栈。
- 通过为一维数组静态分配内存的方式来保存数据。
- 通过为一维数组动态分配内存的方式来保存数据。
为了顺序栈中数据存满时可以对栈进行扩容,在这里,我会采用第2种保存数据的方案来编写顺序栈的实现代码。
此外,为了考虑到元素存取的便利性,将数组下标为0的一端作为栈底最合适。
顺序栈的类定义、初始化和释放操作
我们还是和之前的讲解一样,先说类定义、初始化以及释放操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #define InitSize 10 //动态数组的初始尺寸
#define IncSize 5 //当动态数组存满数据后每次扩容所能多保存的数据元素数量
template <typename T> //T代表数组中元素的类型
class SeqStack
{
public:
SeqStack(int length = InitSize); //构造函数,参数可以有默认值
~SeqStack(); //析构函数
public:
bool Push(const T& e); //入栈(增加数据)
bool Pop(T& e); //出栈(删除数据),也就是删除栈顶数据
bool GetTop(T& e); //读取栈顶元素,但该元素并没有出栈而是依旧在栈中
void DispList(); //输出顺序栈中的所有元素
int ListLength(); //获取顺序栈的长度(实际拥有的元素数量)
bool IsEmpty(); //判断顺序栈是否为空
bool IsFull(); //判断顺序栈是否已满
private:
void IncreaseSize(); //当顺序栈存满数据后可以调用此函数为顺序栈扩容
private:
T* m_data; //存放顺序栈中的元素
int m_maxsize; //动态数组最大容量
int m_top; //栈顶指针(用作数组下标),指向栈顶元素,该值为-1表示空栈
};
//通过构造函数对顺序栈进行初始化
template <typename T>
SeqStack<T>::SeqStack(int length)
{
m_data = new T[length]; //为一维数组动态分配内存,该值和算法空间复杂度无关,空间复杂度一般指算法额外需要的存储空间。
m_maxsize = length; //顺序栈最多可以存储m_maxsize个数据元素
m_top = -1; //空栈
}
//通过析构函数对顺序栈进行资源释放
template <typename T>
SeqStack<T>::~SeqStack()
{
delete[] m_data;
}
|
在main主函数中,加入代码创建一个初始大小为10的顺序栈对象。
1
| SeqStack<int> seqobj(10);
|
在利用上面的代码创建seqobj对象之后,顺序栈看起来就会是图2的样子,此时是一个空栈:
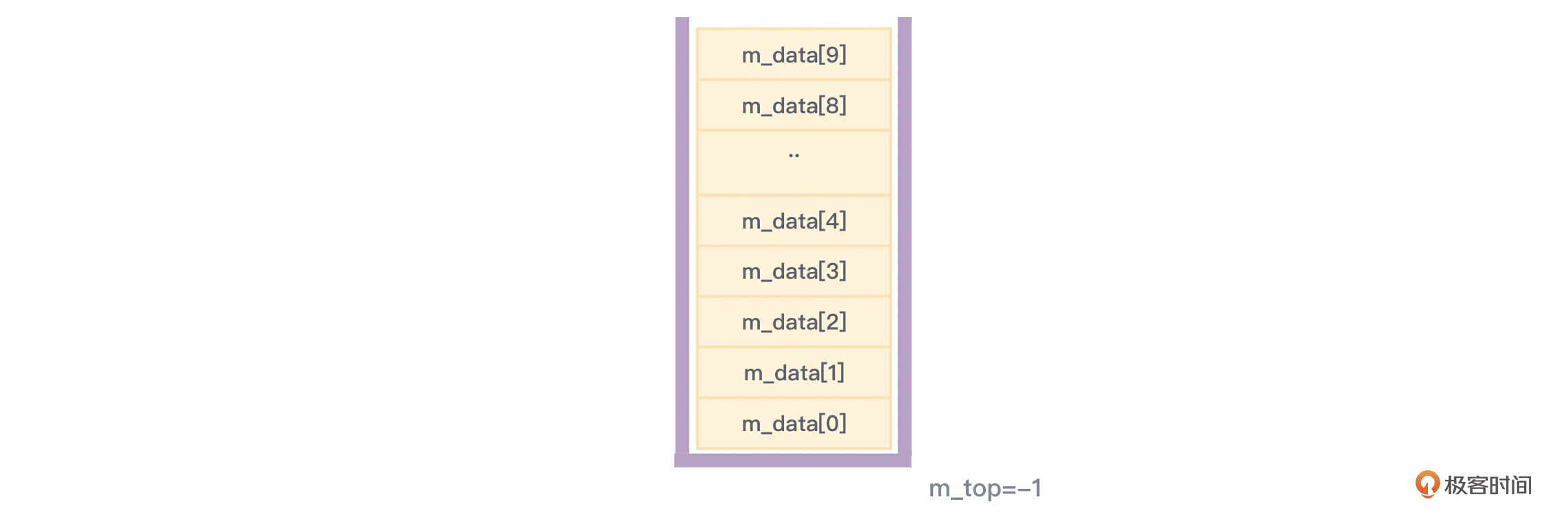
顺序栈的入栈、出栈、获取栈顶元素、显示元素等操作
首先是入栈以及扩容的相关操作。在阅读代码的同时,不要忘了在心里思考一下算法对应的时间复杂度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| //入栈(增加数据),通常时间复杂度为O(1),但一旦需要扩容,时间复杂度就会变成O(n)了
template <typename T>
bool SeqStack<T>::Push(const T& e)
{
if (IsFull() == true)
{
//cout << "顺序栈已满,不能再进行入栈操作了!" << endl;
//return false;
IncreaseSize(); //扩容
}
m_top++; //栈顶指针向后走
m_data[m_top] = e; //本行和上一行可以合并写成一行代码:m_data[++m_top] = e;
return true;
}
//当顺序栈存满数据后可以调用此函数为顺序栈扩容,时间复杂度为O(n)
template<class T>
void SeqStack<T>::IncreaseSize()
{
T* p = m_data;
m_data = new T[m_maxsize + IncSize]; //重新为顺序栈分配更大的内存空间
for (int i = 0; i <= m_top; i++)
{
m_data[i] = p[i]; //将数据复制到新区域
}
m_maxsize = m_maxsize + IncSize; //顺序栈最大长度增加IncSize
delete[] p; //释放原来的内存空间
}
|
其次,就是相应的出栈、读取栈顶元素代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| //出栈(删除数据),也就是删除栈顶数据,时间复杂度为O(1)
template <typename T>
bool SeqStack<T>::Pop(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序栈为空,不能进行出栈操作!" << endl;
return false;
}
e = m_data[m_top]; //栈顶元素值返回到e中。有的实现版本不会在Pop()成员函数中返回栈顶元素,此时要取得栈顶元素需要用到GetTop()成员函数。
m_top--; //本行和上一行可以合并写成一行代码:e = m_data[m_top--];
return true;
}
//读取栈顶元素,但该元素并没有出栈而是依旧在栈顶中,因此m_top值不会发生改变,时间复杂度为O(1)
template <typename T>
bool SeqStack<T>::GetTop(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序栈为空,不能读取栈顶元素!" << endl;
return false;
}
e = m_data[m_top]; //栈顶元素返回到e中。
return true;
}
|
最后,是一些顺序栈的常用操作,比如输出所有元素、获取长度、判断是否为空、是否已满。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| //输出顺序栈中的所有元素,时间复杂度为O(n)
template<class T>
void SeqStack<T>::DispList()
{
//按照从栈顶到栈底的顺序来显示数据
for (int i = m_top; i >= 0; --i)
{
cout << m_data[i] << " "; //每个数据之间以空格分隔
}
cout << endl; //换行
}
//获取顺序栈的长度(实际拥有的元素数量),时间复杂度为O(1)
template<class T>
int SeqStack<T>::ListLength()
{
return m_top+1;
}
//判断顺序栈是否为空,时间复杂度为O(1)
template<class T>
bool SeqStack<T>::IsEmpty()
{
if (m_top == -1)
{
return true;
}
return false;
}
//判断顺序栈是否已满,时间复杂度为O(1)
template<class T>
bool SeqStack<T>::IsFull()
{
if (m_top >= m_maxsize - 1)
{
return true;
}
return false;
}
|
在main主函数中,继续增加下面的代码。
1
2
3
4
5
6
7
8
9
10
| seqobj.Push(150);
seqobj.Push(200);
seqobj.Push(300);
seqobj.Push(400);
seqobj.DispList();
int eval = 0;
seqobj.Pop(eval);
seqobj.Pop(eval);
cout << "---------" << endl;
seqobj.DispList();
|
执行结果如下:

从结果可以看到,程序是先把150、200、300、400进行了入栈操作,此时顺序栈中的数据如图3(a)所示,最先进去的150是在最下面的。然后又将栈顶的两个元素出栈,此时顺序栈中的数据如图3(b)所示。
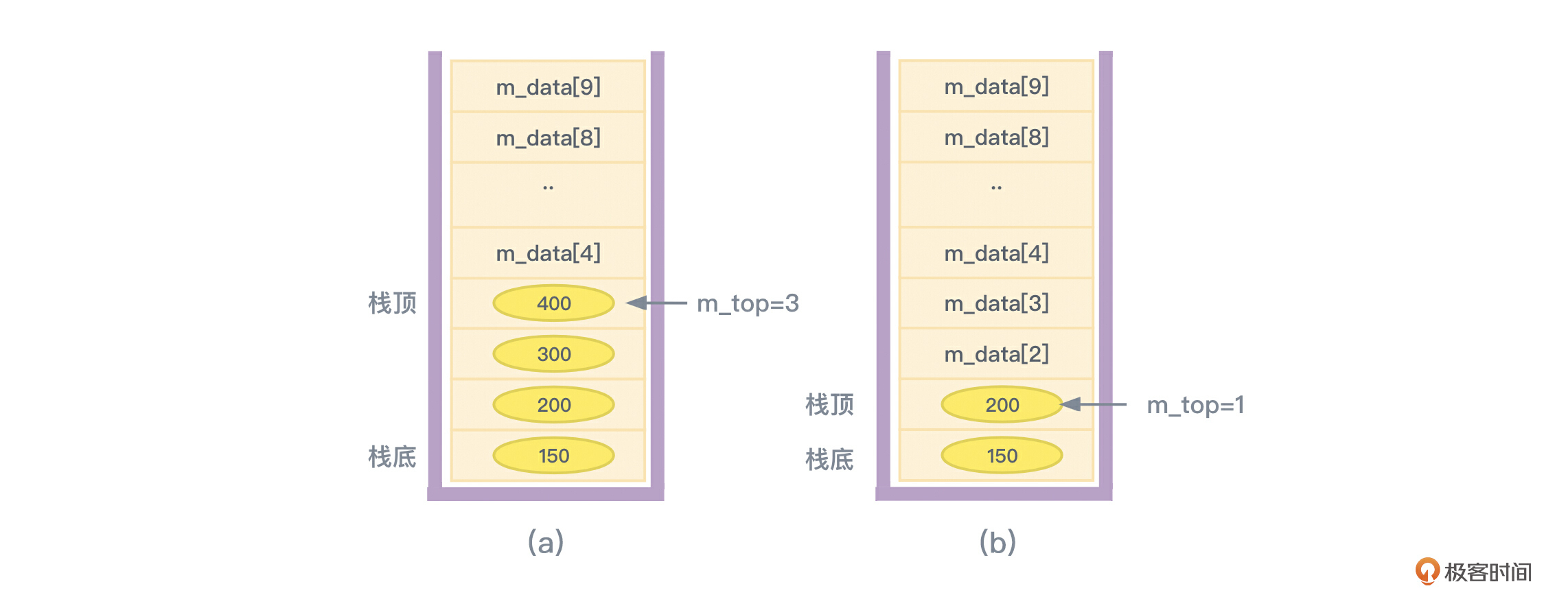
在图3中,先入栈了4个元素,而后又出栈了2个元素,出栈时虽然只修改了m_top栈顶指针,并没有把对应的元素值(m_data[2]和m_data[3])抹除,但这些值已经没有用处了,下次再进行入栈操作的时候会被入栈的新值覆盖。你可以在mian主函数中继续添加下面的代码并跟踪调试看看。
在有的实现栈的范例代码中,会让m_top的初始值等于0(指向0的位置),那么判断栈是否为空的代码(IsEmpty函数)也就是判断m_top是否等于0,而判断栈满(IsFull函数)的条件也应该变成if (m_top >= m_maxsize)。这种实现方式,实际就是让m_top代表下一个可以放入栈中的元素的下标,当数据入栈(Push函数)时,代码行m_top++;和代码行m_data[m_top] = e;的执行就需要互换顺序,而当数据出栈(Pop函数)时,代码行e = m_data[m_top];和代码行m_top–;的执行也需要互换顺序。
共享栈
除了刚才我们提到的常用操作外,这里再补充一个“共享栈”,也就是两个顺序栈共享存储空间。
为什么会提出这个概念呢?之前我们提到的顺序栈,一个比较大的缺点是保存数据的空间初始尺寸不好确定,如果太大,就会浪费空间,如果太小,那么存满数据后再入栈新数据就需要扩容,而扩容就又需要开辟一整块更大的新区域并将原有数据复制到新区域,操作起来比较耗费性能。
不过,我们可以设想一下。假设有两个相同数据类型的顺序栈,如果分别为他们开辟了保存数据的空间,那是不是就可能出现,第一个栈的数据已经存满了而另一个栈中还有很多存储空间的情形呢?那么,如果开辟出来一块保存数据的空间后,让这两个栈同时使用,也就是共享这块空间,是不是也许就能达到最大限度利用这块空间、减少浪费的目的呢?这就是共享栈的含义。
具体如何做到呢?我们还是先从代码层理解一下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| //共享栈
template <typename T> //T代表数组中元素的类型
class ShareStack
{
public:
ShareStack(int length = InitSize) //构造函数,参数可以有默认值
{
m_data = new T[length]; //为一维数组动态分配内存
m_maxsize = length; //共享栈最多可以存储m_maxsize个数据元素
m_top1 = -1; //顺序栈1的栈顶指针为-1,表示空栈
m_top2 = length; //顺序栈2的栈顶指针为length,表示空栈
}
~ShareStack() //析构函数
{
delete[] m_data;
}
public:
bool IsFull() //判断共享栈是否已满
{
if (m_top1 + 1 == m_top2)
{
return true;
}
return false;
}
bool Push(int stackNum,const T& e) //入栈(增加数据),参数stackNum用于标识栈1还是栈2
{
if (IsFull() == true)
{
//共享栈满了,你也可以自行增加代码来支持动态增加共享栈的容量,这里简单处理,直接返回false
cout << "共享栈已满,不能再进行入栈操作了!" << endl;
return false;
}
if (stackNum == 1)
{
//要入的是顺序栈1
m_top1++; //栈顶指针向后走
m_data[m_top1] = e;
}
else
{
//要入的是顺序栈2
m_top2--;
m_data[m_top2] = e;
}
return true;
}
bool Pop(int stackNum, T& e) //出栈(删除数据),也就是删除栈顶数据
{
if (stackNum == 1)
{
//要从顺序栈1出栈
if (m_top1 == -1)
{
cout << "当前顺序栈1为空,不能进行出栈操作!" << endl;
return false;
}
e = m_data[m_top1]; //栈顶元素值返回到e中
m_top1--;
}
else
{
//要从顺序栈2出栈
if (m_top2 == m_maxsize)
{
cout << "当前顺序栈2为空,不能进行出栈操作!" << endl;
return false;
}
e = m_data[m_top2];
m_top2++;
}
return true;
}
private:
T* m_data; //存放共享栈中的元素
int m_maxsize; //动态数组最大容量
int m_top1; //顺序栈1的栈顶指针
int m_top2; //顺序栈2的栈顶指针
};
|
从代码中可以看到,既然是两个顺序栈共享同一块内存空间,那么就需要引入两个栈顶指针(m_top1、m_top2)来分别标识这两个顺序栈的栈顶位置。顺序栈1的栈底位置在最下面,而顺序栈2的栈底位置在最上面。
同时,注意阅读判断共享栈是否已满的代码(IsFull)以及入栈和出栈(Push、Pop)的代码。如果对顺序栈1进行入栈操作,则m_top1要递增,数据要从下向上存储。如果对顺序栈2进行入栈操作,则m_top2要递减,数据从上向下存储。这样的话,从逻辑上看,实现的是两个栈,但这两个栈又是共享着同一块物理内存的,从而提高内存利用率。把它转换成示意图,就会是图4的样子:
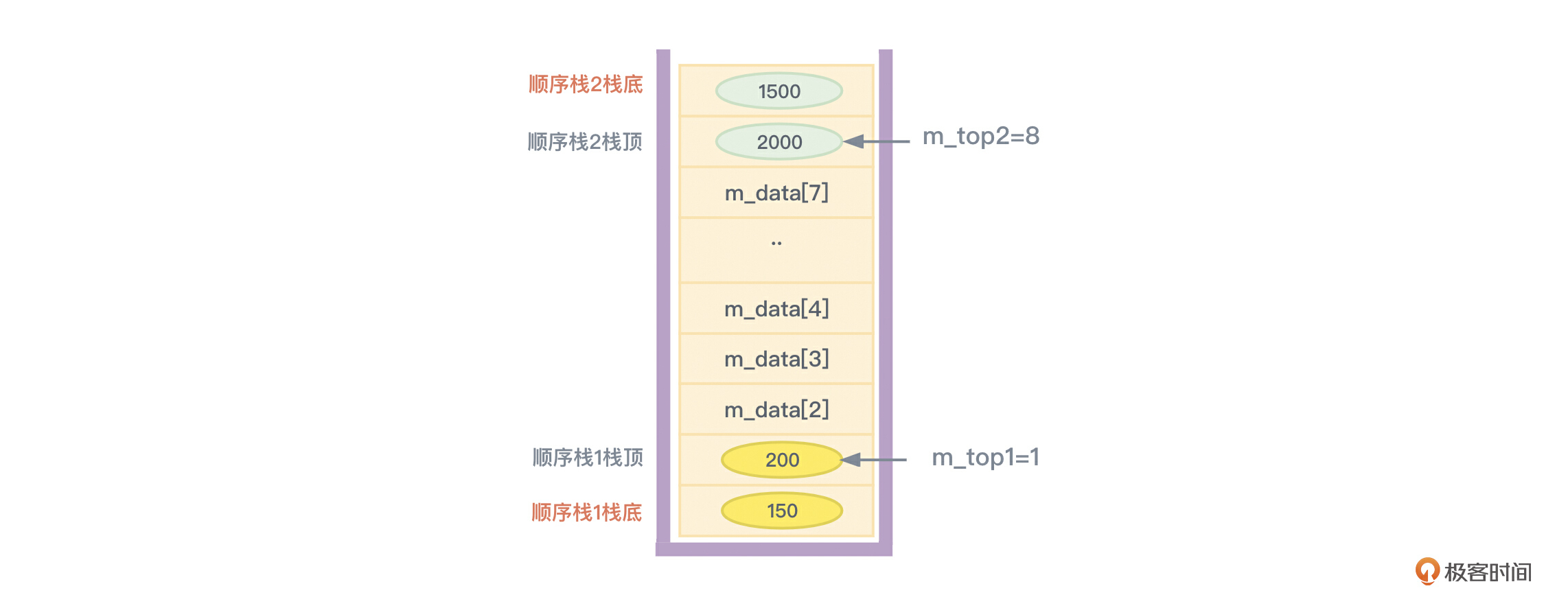
一般来讲,对两个顺序栈的存储空间需求正好相反时,将这两个顺序栈放在一起当作共享栈使用意义才比较大。这里的需求相反,指的就是当一个栈进行入栈操作时,另一个栈同时在进行出栈操作,也就是此消彼长的情况。所以,你也可以把共享栈看成是一种顺序栈的实现技巧。
可以在main主函数中增加下面的代码来测试共享栈。
1
2
3
4
5
6
| ShareStack<int> sharesobj(10);
sharesobj.Push(1, 150);
sharesobj.Push(2, 200);
int eval2;
sharesobj.Pop(1, eval2);
sharesobj.Pop(1, eval2);
|
栈的链式存储(链式栈/链栈)
所谓链式栈,就是链式存储方式来实现的栈。回忆前面讲过单链表的插入操作ListInsert方法,其第一个参数用于指定元素要插入的位置,如果把该参数值设置为1,就是链式栈的入栈操作。对于单链表的删除操作ListDelete方法,其参数用于指定要删除的元素位置,如果把该参数值也设置为1,就是链式栈的出栈操作。
可以看到,链式栈其实就是一个单链表,只不过人为的规定只能在单链表的第一个位置进行插入(入栈)和删除(出栈)操作,即链表头这一端是栈顶。
链式栈的实现代码和单链表的实现代码非常类似,可以把链式栈理解成受限的单链表。在讲解单链表时,可以带头结点也可以不带头节点,但对于链式栈来讲,考虑到只在链表头位置插入数据,所以链式栈一般不需要带头节点。
看一看链式栈的类定义以及常用操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| //链式栈中每个节点的定义
template <typename T> //T代表数据元素的类型
struct StackNode
{
T data; //数据域,存放数据元素
StackNode<T>* next; //指针域,指向下一个同类型(和本节点类型相同)节点
};
//链式栈的定义
template <typename T>
class LinkStack
{
public:
LinkStack(); //构造函数
~LinkStack(); //析构函数
public:
bool Push(const T& e); //入栈元素e
bool Pop(T& e); //出栈(删除数据),也就是删除栈顶数据
bool GetTop(T& e); //读取栈顶元素,但该元素并没有出栈而是依旧在栈中
void DispList(); //输出链式栈中的所有元素
int ListLength(); //获取链式栈的长度
bool Empty(); //判断链式栈是否为空
private:
StackNode<T>* m_top; //栈顶指针
int m_length;//链式栈当前长度
};
//通过构造函数对链式栈进行初始化
template <typename T>
LinkStack<T>::LinkStack()
{
m_top = nullptr;
m_length = 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| //入栈元素e,时间复杂度为O(1)
template <typename T>
bool LinkStack<T>::Push(const T& e)
{
StackNode<T>* node = new StackNode<T>;
node->data = e;
node->next = m_top;
m_top = node;
m_length++;
return true;
}
//出栈(删除数据),也就是删除栈顶数据,时间复杂度为O(1)
template <typename T>
bool LinkStack<T>::Pop(T& e)
{
if (Empty() == true) //链式栈为空
return false;
StackNode<T>* p_willdel = m_top;
m_top = m_top->next;
m_length--;
e = p_willdel->data;
delete p_willdel;
return true;
}
//读取栈顶元素,但该元素并没有出栈而是依旧在栈中
template <typename T>
bool LinkStack<T>::GetTop(T& e)
{
if (Empty() == true) //链式栈为空
return false;
e = m_top->data;
return true;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| //输出链式栈中的所有元素,时间复杂度为O(n)
template<class T>
void LinkStack<T>::DispList()
{
if (Empty() == true) //链式栈为空
return;
StackNode<T>* p = m_top;
while (p != nullptr)
{
cout << p->data << " "; //每个数据之间以空格分隔
p = p->next;
}
cout << endl; //换行
}
//获取链式栈的长度,时间复杂度为O(1)
template<class T>
int LinkStack<T>::ListLength()
{
return m_length;
}
//判断链式栈是否为空,时间复杂度为O(1)
template<class T>
bool LinkStack<T>::Empty()
{
if (m_top == nullptr) //链式栈为空
{
return true;
}
return false;
}
//通过析构函数对链式栈进行资源释放
template <typename T>
LinkStack<T>::~LinkStack()
{
T tmpnousevalue = {0};
while (Pop(tmpnousevalue) == true) {}//把栈顶元素删光,while循环也就退出了,此时也就是空栈了
}
|
在main主函数中,可以加入如下代码进行测试:
1
2
3
4
5
6
7
8
9
10
| LinkStack<int> slinkobj;
slinkobj.Push(12);
slinkobj.Push(24);
slinkobj.Push(48);
slinkobj.Push(100);
slinkobj.DispList();
int eval3 = 0;
slinkobj.Pop(eval3);
slinkobj.DispList();
|
与顺序栈相比,链式栈没有长度限制,不存在内存空间的浪费问题。但对于数据的入栈和出栈这些需要对数据进行定位的操作,顺序栈更加方便,而链式栈中的每个数据节点都需要额外的指针域以指向下一个数据节点,这会略微降低数据的存储效率,当然也会多占用一些内存。所以,如果要存储的数据数量无法提前预估,一般考虑使用链式栈,而如果数据的数量比较固定,可以考虑使用顺序栈。
在前面的讲解中,我们实现了顺序表(以数组的方式),又实现了各种各样的链表。在这节课,我们也通过数组的方式实现了顺序栈,通过单链表实现了链式栈。所以,把顺序栈看成是功能受限的数组,或把链式栈看成是功能受限的单链表,都是没有问题的。
可能你会认为,既然已经存在数组和单链表,直接使用不是更方便,为什么又创造出功能受限的栈来呢?你可以理解为,因为功能受限,所以使用起来也更加简单,错用误用的概率比数组、单链表等更低。
栈有很多应用,比如很多人都知道的在函数调用期间需要用栈来保存临时的参数信息、函数内局部变量信息、函数调用返回地址信息等。网上也有很多小例子演示栈的简单应用,比如利用栈来进行括号匹配的检验,利用栈来计算表达式结果等。有兴趣的话,你可以通过搜索引擎自行搜索了解。在后续的课程中,我也会用栈来实现诸如树的非递归遍历、记录节点路径信息等操作,相信那时你会对栈的应用有更深刻的理解。
小结
这节课,我们讲解了栈这种常用的数据结构,分别用代码实现了顺序栈(包括共享栈)和链栈,同时针对栈的应用举了几个小例子。
栈的应用场合其实很多,上面也只是列举了几个范例进行简单演示,更多的案例需要你在实践中学习和体会。在实际应用中,有时为达到简化计算步骤的目的,还可以根据算法的需要引入两个甚至更多的栈来参与计算,每个栈都有各自的目的和分工,这都很平常,也不必觉得奇怪。后面的课程中,我们也会经常用到栈这种数据结构,届时你对栈的应用也会有更深层次的理解。
通过今天这一讲,你会发现,“在某一个事物的进行中需要保存一些数据,而将来又会以相反的顺序取回”这样的场合里,总会有“栈”的身影。
在STL(标准模板库)中,提供了一个名字叫做stack的容器,该容器其实是一个类模板,这个类模板实现的就是栈的功能,所以通常情况下不需要你自己写栈的实现代码,用这个现成的即可。而这节课的内容,就可以让你对栈的理解更深入,从而更好地使用stack容器。
课后思考
在这节课的最后,我也给你留了几道思考题,可以想一想。
- 回忆一下你曾经在哪些场合使用过栈或遇到过对栈的应用,试着列举出一二。
- 如果你有兴趣可以对stack容器的源码做适当的研究,当然,其源码比较繁琐和复杂,需要你有比较好的模板与泛型编程基础才能读懂。
- 这节课讲的栈是一种数据结构。但从操作系统层面,也有栈这个概念,只不过操作系统层面所指的栈和我们这里所讲的栈不是同一个意思。有兴趣了解的话,可以在搜索引擎中输入“堆和栈的区别”这样的关键词来了解操作系统层面的栈指的是什么意思。
欢迎你在留言区和我互动。如果觉得有所收获,也可以把课程分享给更多的同学一起交流学习,我们下节课见!





