你好,我是王健伟。
上节课我们提到的“栈”,用的是“桶”和“抽屉”做类比,实现的是先进后出。这节课我们来聊“队列”,根据名字想象一下,它实现的是不是先进先出了呢?
是的。队列也是一种受限的线性表,它的特点是在一端进行插入操作,在另一端进行删除操作(与栈刚好相反)。把允许进行插入操作的一端称为队尾,允许删除操作的一端称为队头。
把队列想象成人们排队购物,排在队伍第一位的人最先购买然后最先离开,而排在队伍最后一位的人最后购买最后离开。我们向队列中插入元素,就叫做入队,从队列中删除元素,叫做出队。不包含任何数据的队列,就是空队列。
队列也被称为先进先出(First In First Out:FIFO)的线性表。换句话说,插入数据只能在队尾(队列尾部)进行,删除数据只能在队头(队列头部)进行。
用队列存取数据的示意图,如图1所示:

如果我们分别将数据a1、a2、a3、a4、a5入队,那么在将数据出队的时候,顺序同样是a1、a2、a3、a4、a5,和入队顺序是一样的。
队列支持的操作和栈非常类似,一般包括队列的创建、入队(插入/增加数据)、出队(删除数据)、获取队头元素(查找数据)、判断队列是否为空或者是否已满等等操作。
接下来,我们就看下这些操作的实现。
队列的顺序存储(顺序队列)
所谓顺序队列,就是顺序存储,也就是用一段连续的内存空间,去依次存储队列中的数据。和顺序栈一样,为了数据存满时可以对队列进行扩容,顺序队列也会采用为一维数组动态分配内存的方案来编写实现代码。
基础实现代码
先来看一些基础的实现代码:类定义、初始化以及释放操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #define MaxSize 10 //数组的尺寸
template <typename T> //T代表数组中元素的类型
class SeqQueue
{
public:
SeqQueue(); //构造函数
~SeqQueue(); //析构函数
public:
bool EnQueue(const T& e); //入队列(增加数据)
bool DeQueue(T& e); //出队列(删除数据)
bool GetHead(T& e); //读取队头元素,但该元素并没有出队列而是依旧在队列中
void ClearQueue(); //将队列清空
void DispList(); //输出顺序队列中的所有元素
int ListLength(); //获取顺序队列的长度(实际拥有的元素数量)
bool IsEmpty(); //判断顺序队列是否为空
bool IsFull(); //判断顺序队列是否已满
private:
T* m_data; //存放顺序队列中的元素
int m_front; //队头指针(数组下标),允许删除的一端,如果队列不为空,则指向队列头元素
int m_rear; //队尾指针(数组下标),允许插入的一端 ,如果队列不为空,则指向队尾元素的下一个位置
};
//通过构造函数对顺序队列进行初始化
template <typename T>
SeqQueue<T>::SeqQueue()
{
m_data = new T[MaxSize]; //为一维数组动态分配内存
//空队列约定m_front和m_rear都为0
m_front = 0;
m_rear = 0;
}
//通过析构函数对顺序队列进行资源释放
template <typename T>
SeqQueue<T>::~SeqQueue()
{
delete[] m_data;
}
|
之后,就是入队列、出队列、读取队头元素操作代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| //入队列(增加数据),也就是从队尾增加数据
template <typename T>
bool SeqQueue<T>::EnQueue(const T& e)
{
if (IsFull() == true)
{
cout << "顺序队列已满,不能再进行入队操作了!" << endl;
return false;
}
m_data[m_rear] = e; //将数据放入队尾
m_rear++;//队尾指针向后走,本行和上一行可以合并写成一行代码:m_data[m_rear++] = e;
return true;
}
//出队列(删除数据),也就是删除队头数据
template <typename T>
bool SeqQueue<T>::DeQueue(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序队列为空,不能进行出队操作!" << endl;
return false;
}
e = m_data[m_front]; //队头元素值返回到e中。
m_front++;//本行和上一行可以合并写成一行代码:e = m_data[m_front++];
return true;
}
//读取队头元素,但该元素并没有出队列而是依旧在队列中
template <typename T>
bool SeqQueue<T>::GetHead(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序队列为空,不能读取队头元素!" << endl;
return false;
}
e = m_data[m_front]; //队头元素返回到e中。
return true;
}
|
最后,是一些顺序队列的常用操作,比如输出所有元素、获取长度、判断是否为空、是否已满、将队列清空。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| //输出顺序队列中的所有元素,时间复杂度为O(n)
template<class T>
void SeqQueue<T>::DispList()
{
//按照从队头到队尾的顺序来显示数据
for (int i = m_front; i < m_rear ; ++i)
{
cout << m_data[i] << " "; //每个数据之间以空格分隔
}
cout << endl; //换行
}
//获取顺序队列的长度(实际拥有的元素数量),时间复杂度为O(1)
template<class T>
int SeqQueue<T>::ListLength()
{
return m_rear - m_front;
}
//判断顺序队列是否为空,时间复杂度为O(1)
template<class T>
bool SeqQueue<T>::IsEmpty()
{
if (m_front == m_rear)
{
return true;
}
return false;
}
//判断顺序队列是否已满,时间复杂度为O(1)
template<class T>
bool SeqQueue<T>::IsFull()
{
if(m_rear >= MaxSize) //队尾指针和数组容量做比较
{
return true;
}
return false;
}
//将队列清空
template<class T>
void SeqQueue<T>::ClearQueue()
{
m_front = m_rear = 0;
}
|
在main主函数中,我们可以加入下面的测试代码,实现4个数据的入队列。
1
2
3
4
5
6
| SeqQueue<int> seqobj;
seqobj.EnQueue(150);
seqobj.EnQueue(200);
seqobj.EnQueue(300);
seqobj.EnQueue(400);
seqobj.DispList();
|
执行结果为:

此时,队列的情形如2所示:
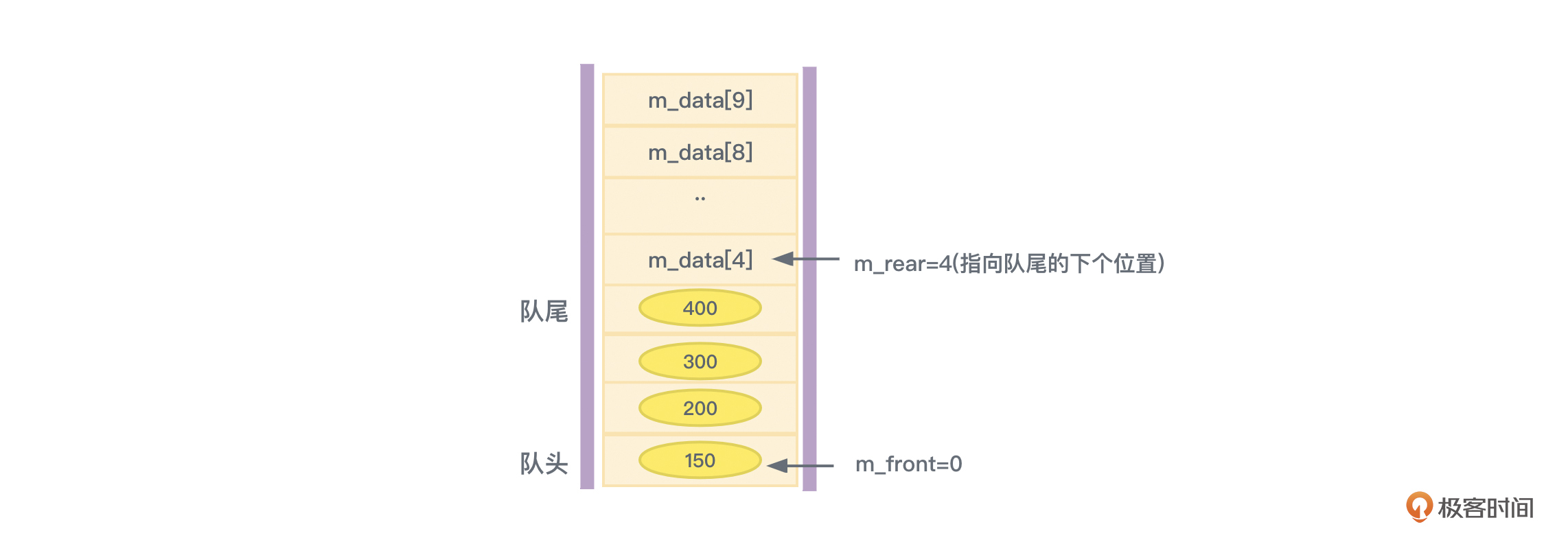
之后,我们可以继续在main中加入下面的代码来将2个元素出队。
1
2
3
4
5
| cout << "---------" << endl;
int eval = 0;
seqobj.DeQueue(eval);
seqobj.DeQueue(eval);
seqobj.DispList();
|
新增代码的执行结果如下:

从结果中可以看到,队头的两个元素出队(被删除)了,此时,队列的情形如图3所示:
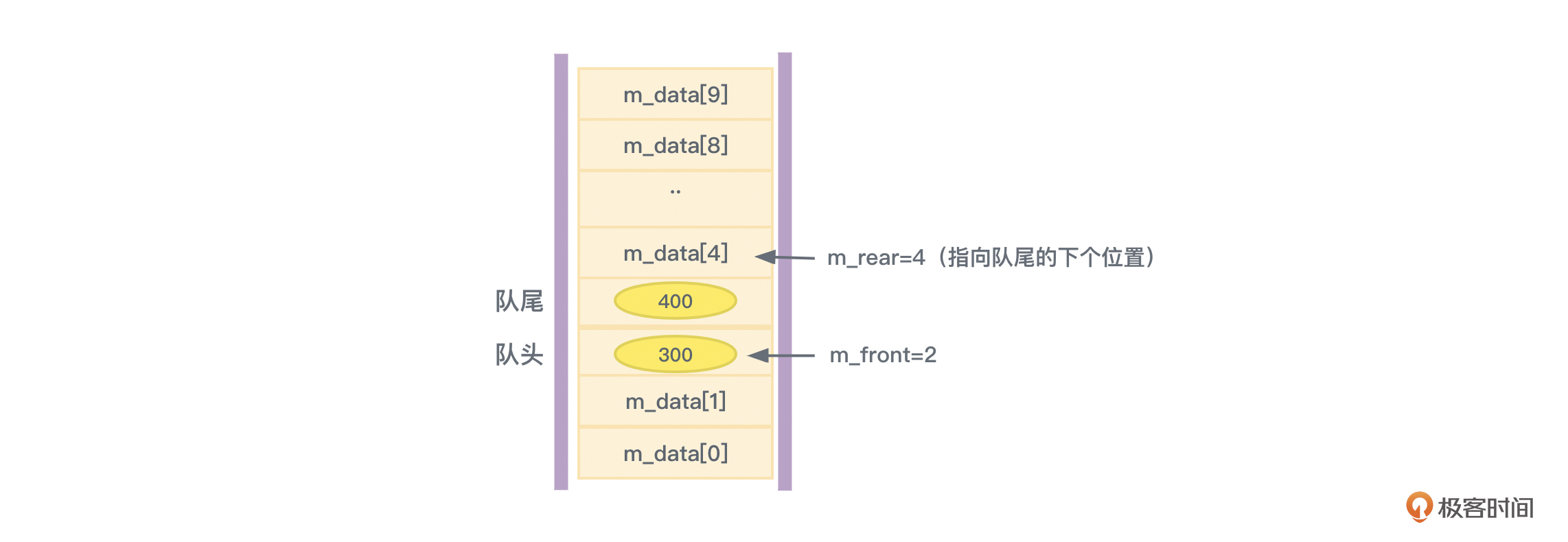
从图3可以看到,将两个元素出队后,队头指针m_front从0变成了2。而此时m_data[0]和m_data[1]这两个能够容纳元素的位置实际上是空出来了。但如果此时继续将新的元素入队,那么m_rear值会不断增加,元素会被继续放入m_data[4]、m_data[5]、m_data[6]… m_data[9]等位置。
试想,当m_data[9]被放入了元素后,继续向队列中放入元素,就会导致IsFull成员函数返回true,意味着队列已满,无法入队更多元素,而实际上此时m_data[0]和m_data[1]这两个位置还是可以容纳两个元素的。所以,此时队列的满,是一种虚假的满。
那要如何解决这个问题呢?也许你会想在入队并发现数组头还有空闲位置的时候,通过数据搬运的方式来填补空闲位置,不过这并不是一个好办法,会大大增加入队的时间复杂度,所以解决的办法是对上述代码做适当改进,引入循环队列的概念。
循环队列
什么是循环队列?在图3中,即便IsFull成员函数返回true,但实际上队列也并没有满。因为m_data[0]和m_data[1]这两个位置还是可以容纳新元素的。所以必须让m_rear指针指回到m_data[0]去,这样才可以继续从m_data[0]开始保存新元素。
为了做到这一点,我们可以修改EnQueue这个入队成员函数,下面是修改后的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| //入队列(增加数据),也就是从队尾增加数据
template <typename T>
bool SeqQueue<T>::EnQueue(const T& e)
{
if (IsFull() == true)
{
cout << "顺序队列已满,不能再进行入队操作了!" << endl;
return false;
}
m_data[m_rear] = e; //将数据放入队尾
//m_rear++; //队尾指针向后走,本行和上一行可以合并写成一行代码:m_data[m_rear++] = e;
m_rear = (m_rear + 1) % MaxSize; //队尾指针加1并取余,这样m_data的下标就控制在了0到(MaxSize-1)之间了
return true;
}
|
可以看到,这里是对m_rear这个队尾指针加1后取余,这样,当m_rear到达9(MaxSize-1)后再次入队元素时,m_rear就会变为0,就正好可以在m_data[0]这个位置继续保存新入队的元素。
换句话说,此时随着新元素的入队,在队列不满的情况下,m_rear值的变化就是从0到9,然后再变回0,不断增加到9……如此反复。显然,我们可以把顺序队列看成是一个环状的队列,队列首尾相连,保存数据元素的空间就好像是一个环状空间,这种头尾相接的队列,就叫做循环队列。
之后,继续在main中加入代码行来向队列中继续增加5个元素。
1
2
3
4
5
6
7
| cout << "---------" << endl;
seqobj.EnQueue(500);
seqobj.EnQueue(600);
seqobj.EnQueue(700);
seqobj.EnQueue(800);
seqobj.EnQueue(900);
seqobj.DispList();
|
新增代码的执行结果如下:

此时的循环队列示意图,如图4所示:
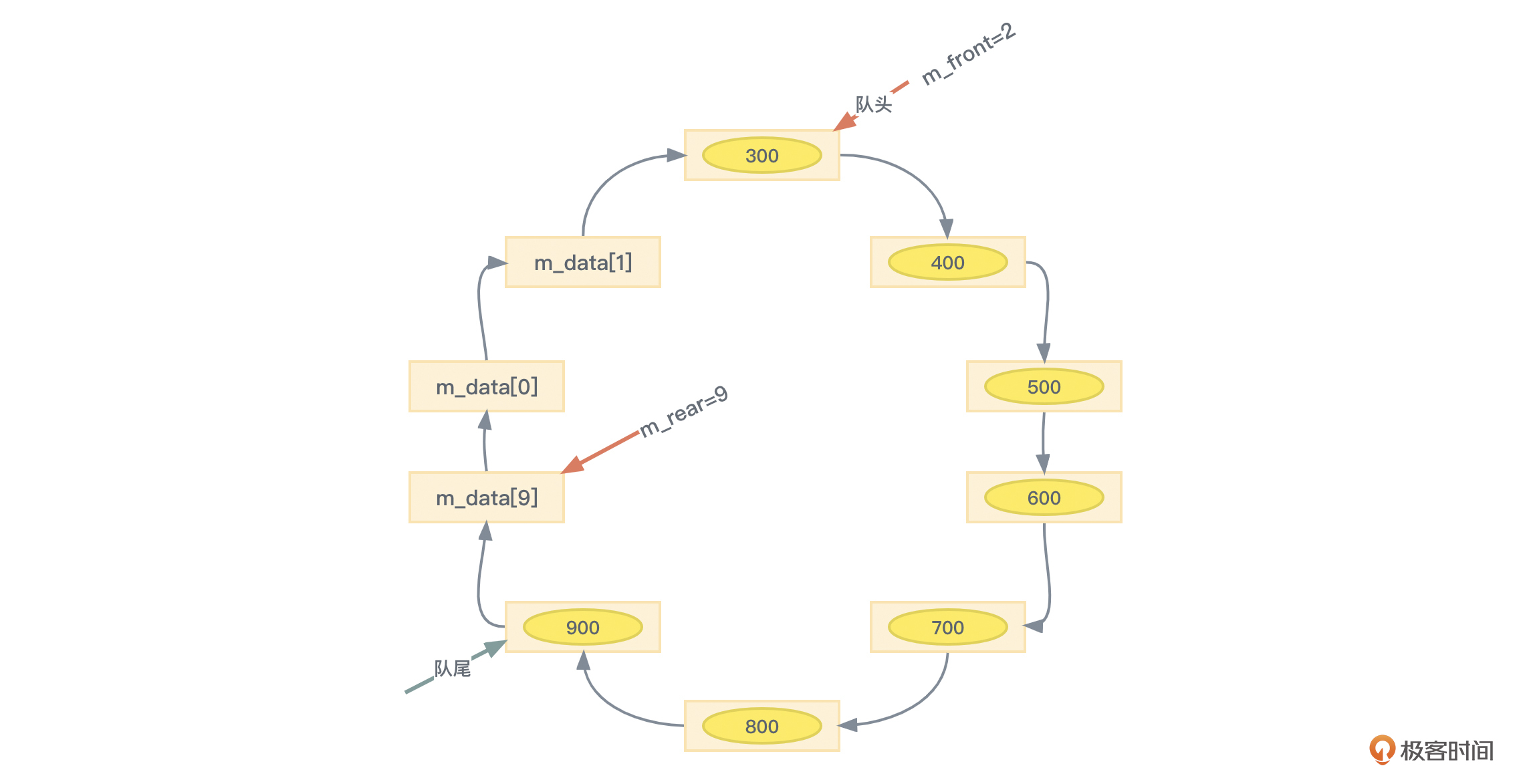
如果此时再入队1个元素,那么这个元素将保存在m_data[9]的位置且m_rear将等于0。这样再次入队新元素时,m_data[0]、m_data[1]这样的空闲位置就可以被使用了。
不过,问题又来了。要怎么判断循环队列什么时候满了呢?目前判断队列是否已满的成员函数IsFull的判满条件是只要m_rear >= MaxSize,也就是只要队尾指针达到了数组容量,就认为队列满了,这显然不行。我们之前已经看到,m_rear的值因为取余的原因,永远都小于MaxSize,也就是队列永远不会满,这显然是不对的。
想象一下,如果把图4中的m_data[0]到m_data[9]全部存满数据,那队列显然就是满的了,此时m_rear == m_front就会成立。我们知道,判断队列是否为空的成员函数IsEmpty的判断条件同样是m_front == m_rear,这意味着判断队列空和队列满的代码是相同的,这是不可以的。
为此,一个比较常用的判断循环队列是否满的方法,就是通过牺牲一个保存元素的空间来判断,如图5所示:
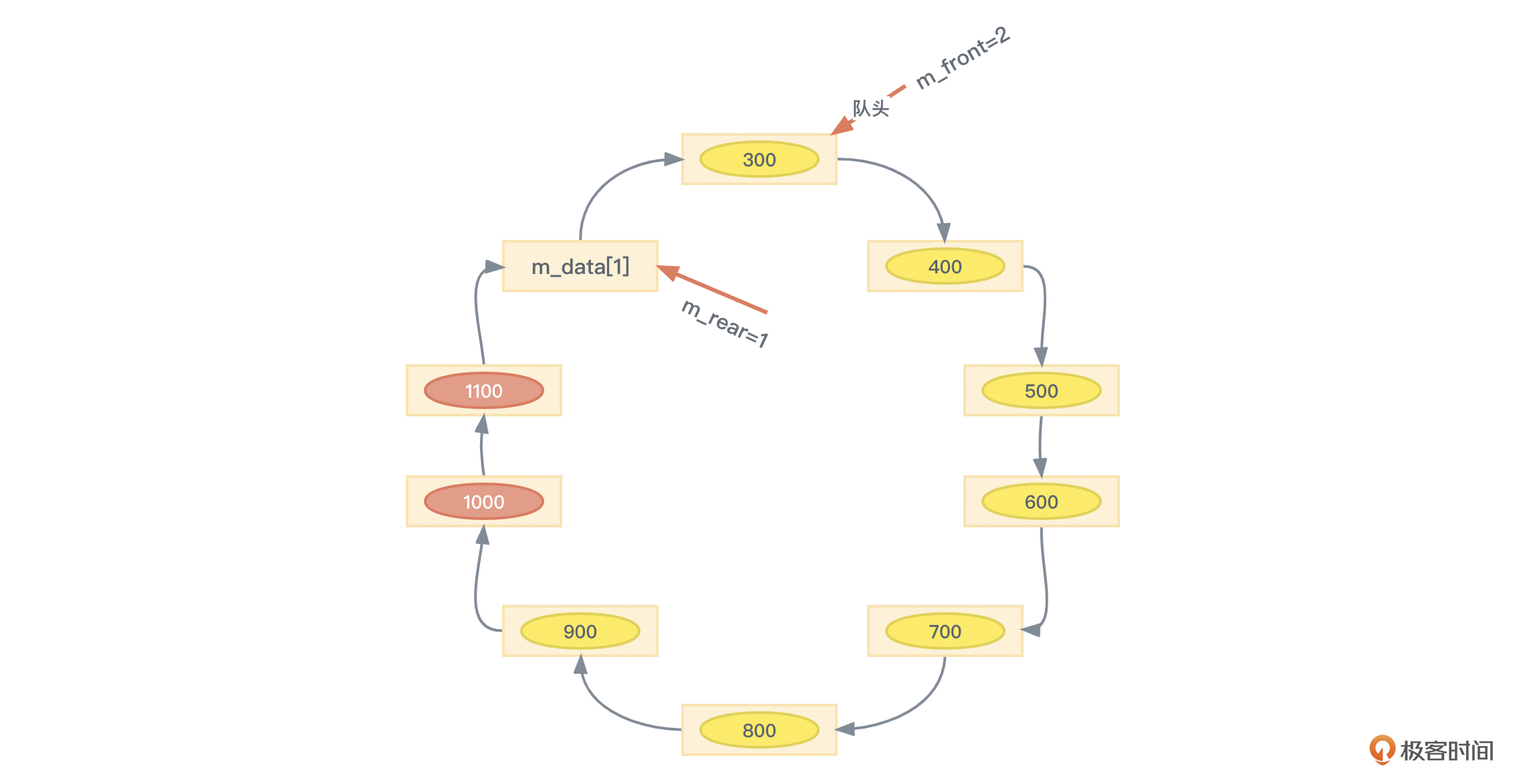
你看,在图5中,队列中一共有10个位置,但只保存了9个元素,留出了1个空闲位置不允许插入元素,这个时候,就满足条件m_rear+1 == m_front,或者更严谨地说,应该是(m_rear + 1) % MaxSize == m_front,也就是说,当该条件成立时,就认为队列满了(即使该队列还有一个空闲位置)。
下面是修改后的IsFull成员函数代码。
1
2
3
4
5
6
7
8
9
10
11
| //判断顺序队列是否已满,时间复杂度为O(1)
template<class T>
bool SeqQueue<T>::IsFull()
{
//if(m_rear >= MaxSize) //队尾指针和数组容量做比较
if((m_rear + 1) % MaxSize == m_front)
{
return true;
}
return false;
}
|
当然,出队列成员函数DeQueue也必须做出修改以控制m_front的取值范围,下面是修改后的代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| //出队列(删除数据),也就是删除队头数据
template <typename T>
bool SeqQueue<T>::DeQueue(T& e)
{
if (IsEmpty() == true)
{
cout << "当前顺序队列为空,不能进行出队操作!" << endl;
return false;
}
e = m_data[m_front]; //队头元素值返回到e中。
//m_front++;//本行和上一行可以合并写成一行代码:e = m_data[m_front++];
m_front = (m_front +1) % MaxSize; //队头指针加1并取余
return true;
}
|
其他一些需要修改的成员函数代码这里也给出了参考。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| //获取顺序队列的长度(实际拥有的元素数量),时间复杂度为O(1)
template<class T>
int SeqQueue<T>::ListLength()
{
//return m_rear - m_front;
return (m_rear + MaxSize - m_front) % MaxSize;
}
//输出顺序队列中的所有元素,时间复杂度为O(n)
template<class T>
void SeqQueue<T>::DispList()
{
//按照从队头到队尾的顺序来显示数据
//for (int i = m_front; i < m_rear ; ++i)
for (int i = m_front; i != m_rear;)
{
cout << m_data[i] << " "; //每个数据之间以空格分隔
i = (i + 1) % MaxSize;
}
cout << endl; //换行
}
|
如果你认为,就为了判断队列是不是满了,就浪费了一个空闲队列的位置,实在是不值得,那么你还可以引入其他的方法,这里列举两种。
- 引入一个int类型的成员变量m_size,初始值为0,当成功入队列一个元素时,m_size自加1,当成功出队列一个元素时,m_size自减1,那么,就可以通过m_size的值来判断队列是满还是空了(m_size==0为空,m_size== MaxSize为满)。
- 引入一个char(一个字节够了)类型的成员变量m_tag,初始值为0。当执行出队列(删除)操作时,把该变量的值设置为0,当执行入队列(插入)操作时,把该变量的值设置为1,这样就标记了最近是执行了删除操作还是插入操作。注意,只有出队列操作才会导致队列为空,只有入队列操作才会导致队列变满,所以,代码大概就会是下面的样子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| template <typename T>
bool SeqQueue<T>::EnQueue(const T& e) //入队列操作
{
if (IsFull() == true)
{
cout << "顺序队列已满,不能再进行入队操作了!" << endl;
return false;
}
m_tag = 1; //入队
......
}
template<class T>
bool SeqQueue<T>::IsFull()//判断顺序队列是否已满
{
if (m_front == m_rear && tag == 1)
return true;
return false;
}
template <typename T>
bool SeqQueue<T>::DeQueue(T& e) //出队列操作
{
if (IsEmpty() == true)
{
cout << "顺序队列为空,不能进行出队操作!" << endl;
return false;
}
m_tag = 0; //出队
......
}
template<class T>
bool SeqQueue<T>::IsEmpty()//判断顺序队列是否为空
{
if (m_front == m_rear && tag == 0)
{
return true;
}
return false;
}
|
队列的链式存储(链式队列)
一般来讲,如果队列长度的最大值比较确定的情况下,可以考虑使用顺序队列(循环队列),否则,就可以考虑使用链式队列了。
所谓链式队列,就是用链式存储的方式来实现的队列。你可以把它理解成一个操作受限的单链表,只允许在尾部插入元素,只允许在头部删除元素。之前学习过单链表的你,这里再学习链式队列,就会非常容易。
和单链表一样,链式队列可以带头结点,也可以不带头结点,同样为编程方便,这里我会采用带头节点的实现方式去讲解。
先来看一些基础的实现代码。先说类定义、初始化以及释放操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| //链式队列中每个节点的定义
template <typename T> //T代表数据元素的类型
struct QueueNode
{
T data; //数据域,存放数据元素
QueueNode<T>* next; //指针域,指向下一个同类型(和本节点类型相同)节点
};
//链式队列的定义
template <typename T> //T代表数组中元素的类型
class LinkQueue
{
public:
LinkQueue(); //构造函数
~LinkQueue(); //析构函数
public:
bool EnQueue(const T& e); //入队列(增加数据)
bool DeQueue(T& e); //出队列(删除数据)
bool GetHead(T& e); //读取队头元素,但该元素并没有出队列而是依旧在队列中
void DispList(); //输出链式队列中的所有元素
int ListLength(); //获取链式队列的长度(实际拥有的元素数量)
bool IsEmpty(); //判断链式队列是否为空
private:
QueueNode<T>* m_front; //头指针(指向头结点),这一端允许出队(删除)
QueueNode<T>* m_rear; //专门引入尾指针以方便入队(插入)操作
int m_length; //记录长度,方便获取长度
};
//通过构造函数对链式队列进行初始化
template <typename T>
LinkQueue<T>::LinkQueue()
{
m_front = new QueueNode<T>; //先创建一个头结点
m_front->next = nullptr;
m_rear = m_front;
m_length = 0;
//若不带头节点的链式队列初始化代码应该如下,供参考
/*m_front = nullptr;
m_rear = nullptr;*/
}
//通过析构函数对链式队列进行资源释放
template <typename T>
LinkQueue<T>::~LinkQueue()
{
QueueNode<T>* pnode = m_front->next;
QueueNode<T>* ptmp;
while (pnode != nullptr) //该循环负责释放数据节点
{
ptmp = pnode;
pnode = pnode->next;
delete ptmp;
}
delete m_front; //释放头结点
m_front = m_rear = nullptr; //非必须
m_length = 0; //非必须
}
|
之后,就是入队列、出队列、读取队头元素操作代码。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| //入队列(增加数据),也就是从队尾增加数据
template <typename T>
bool LinkQueue<T>::EnQueue(const T& e)
{
QueueNode<T>* node = new QueueNode<T>;
node->data = e;
node->next = nullptr;
m_rear->next = node; //新节点插入到m_rear后面
m_rear = node; //更新队列尾指针
m_length++;
return true;
}
//出队列(删除数据),也就是删除队头数据
template <typename T>
bool LinkQueue<T>::DeQueue(T& e)
{
if (IsEmpty() == true)
{
cout << "当前链式队列为空,不能进行出队操作!" << endl;
return false;
}
QueueNode<T>* p_willdel = m_front->next;
e = p_willdel->data;
m_front->next = p_willdel->next;
if (m_rear == p_willdel) //队列中只有一个元素节点(被删除后,整个队列就为空了)
m_rear = m_front; //设置队列为空(尾指针指向头指针)
delete p_willdel;
m_length--;
return true;
}
//读取队头元素,但该元素并没有出队列而是依旧在队列中
template <typename T>
bool LinkQueue<T>::GetHead(T& e)
{
if (IsEmpty() == true)
{
cout << "当前链式队列为空,不能读取队头元素!" << endl;
return false;
}
e = m_front->next->data;
return true;
}
|
最后,是一些链式队列的常用操作,比如输出所有元素、获取长度、判断是否为空。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| //输出链式队列中的所有元素,时间复杂度为O(n)
template<class T>
void LinkQueue<T>::DispList()
{
QueueNode<T>* p = m_front->next;
while (p != nullptr)
{
cout << p->data << " "; //每个数据之间以空格分隔
p = p->next;
}
cout << endl; //换行
}
//获取链式队列的长度(实际拥有的元素数量),时间复杂度为O(1)
template<class T>
int LinkQueue<T>::ListLength()
{
return m_length;
}
//判断链式队列是否为空,时间复杂度为O(1)
template<class T>
bool LinkQueue<T>::IsEmpty()
{
//当然,换一种判断方式也行:if(m_front->next == nullptr) return true;
if (m_front == m_rear)
{
return true;
}
return false;
}
|
之后,在main中加入代码行。
1
2
3
4
5
6
7
8
| LinkQueue<int> lnobj;
lnobj.EnQueue(150);
int eval2 = 0;
lnobj.DeQueue(eval2);
lnobj.EnQueue(200);
lnobj.EnQueue(700);
lnobj.DispList();
|
执行结果为:

从代码中可以看到,引入的两个指针,分别是头指针和尾指针。在构造函数中,需要将这两个指针进行初始化,初始化后的头尾指针分别指向头结点,这也意味着此时该链式队列为空,如图6所示:

入队新元素需要在链的末尾(队尾)进行。图7是入队两个元素的情形,注意,尾指针始终要保持指向最后一个元素节点。
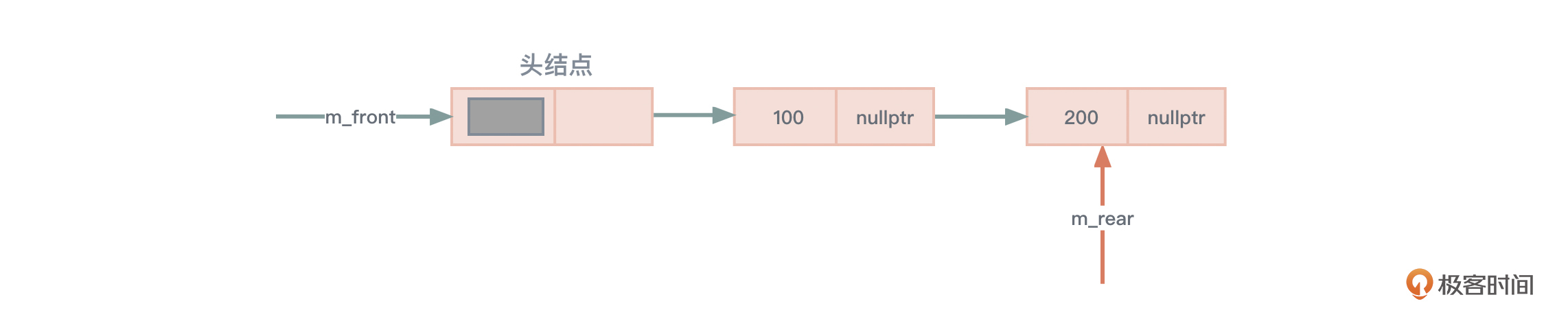
代码中引入了成员变量m_length以快速获取队列的长度(通过成员函数ListLength),时间复杂度仅为O(1),如果用传统的从头指针遍历到尾指针的方法来计算队列长度,那么时间复杂度就会变成O(n)。所以,如果需要频繁获取队列长度,引入m_length就会明显提升效率。
另一个值得说的是,顺序队列存在队列满的问题,而链式队列因为是通过new来创建元素节点,所以不存在队列满的问题,除非物理内存不足。而如果不是软件导致内存泄漏,通常物理内存不会不足,一旦物理内存不足,就会导致整个程序运行崩溃,此时必须全面对程序进行排错。
双端队列
前面所讨论的顺序或者链式队列可以看成是普通队列,其实,还有一些变种的队列——双端队列。双端队列允许在两端插入数据,也允许在两端删除数据。它的存取数据示意图,如图8所示:

当然,我们也可以对双端队列存取数据进行一定的限制,这样就可以得到“输入受限的双端队列”和“输出受限的双端队列”两种情况。
所谓输入受限的双端队列,指的是数据只能从一端插入但可以从两端删除的双端队列,如图9所示:

而输出受限的双端队列,指的是数据可以从两端插入但只能从一端删除的双端队列,如图10所示:

从功能上来讲,双端队列的功能既包括了栈功能,又包括了队列功能,灵活性大大增强,但从实用性来讲,人们更经常使用的是栈和普通队列而不是双端队列。有兴趣的话,你也可以利用前面学习过的知识,尝试实现自己的双端队列。
小结
这节课,我们学习了队列这种常用的数据结构,分别用代码实现了队列的顺序存储(顺序队列)和链式存储(链式队列)。此外,还引出了双端队列的概念。在后面的课程中,会多次用到队列这种数据结构来保存数据,相信那时你会对队列的用途有更深刻的理解。
队列是一种与栈相对的数据结构,之所以这样讲,是因为栈是一种后进先出的数据结构,而队列是一种先进先出的数据结构。
队列的应用十分广泛,这里我们举两个典型应用的例子。
- 去营业大厅办理业务时使用的叫号系统就是一个队列,办理业务的人要先取号后等待叫号,号码按照取号的顺序保存在队列中,叫号时最先取号的人会被最先叫到。
- 多人同时使用网络打印机打印文件,因为打印机的速度很慢,所以每个人提交的打印任务需要在一个队列中进行排队(打印队列),打印机根据先进先出(先来先服务)的原则,依次从打印队列中取出打印任务并进行打印工作。
其实,对于许多服务资源有限的场合,都可以通过队列来实现对服务请求的排队。
在STL(标准模板库)中,提供了一个名字叫做queue的容器,该容器实现了队列的功能,有兴趣可以对其源码做适当研究。队列同栈一样,也分为顺序存储和链式存储。同样,STL中也提供了名字叫做deque的容器——一个典型的双端队列,有兴趣的话,你也可以读一读它的实现代码。
归纳思考
你可以使用一下STL中提供的deque容器,了解一下它提供的各种调用接口,参考这些调用接口,自己尝试实现一个双端队列。
欢迎你在留言区和我分享实践的成果,如果觉得有所收获,也可以把课程分享给更多的朋友一起学习进步,我们下节课见!













