4、单链表：如何通过指针提升插入、删除数据的速度

你好，我是王健伟。

今天我继续说一说“单链表”。

上节课我们提到过，顺序表（线性表的顺序存储）的最大缺点是，在插入和删除操作可能会移动大量元素，去保证元素之间的内存不能有空隙，而这，会导致程序的执行效率变低。

那我们要如何弥补这个缺点呢？这就涉及到了我们今天的内容：采用线性表的链式存储来保存数据元素。

线性表的链式存储也非常基础和常用，它不需要使用连续的内存空间。从名字可以得知，所谓链式存储，是通过“链（指针）”建立元素之间的关系，保证元素之间像一条线一样按顺序排列。这样，在插入和删除元素的时候，就不需要为了保证内存空间的连续性，去进行数据元素的大量迁移，只需要修改指向元素的指针即可。

用链式存储实现的线性表叫做链表，链表比顺序表稍复杂一些。它可以具体分为单链表、双链表、循环链表、静态链表这四种。这节课，我们先讲解单链表。

单链表有哪些特点？

图1展示了顺序表与单链表保存数据元素的区别（左侧为顺序表，右侧为单链表）。

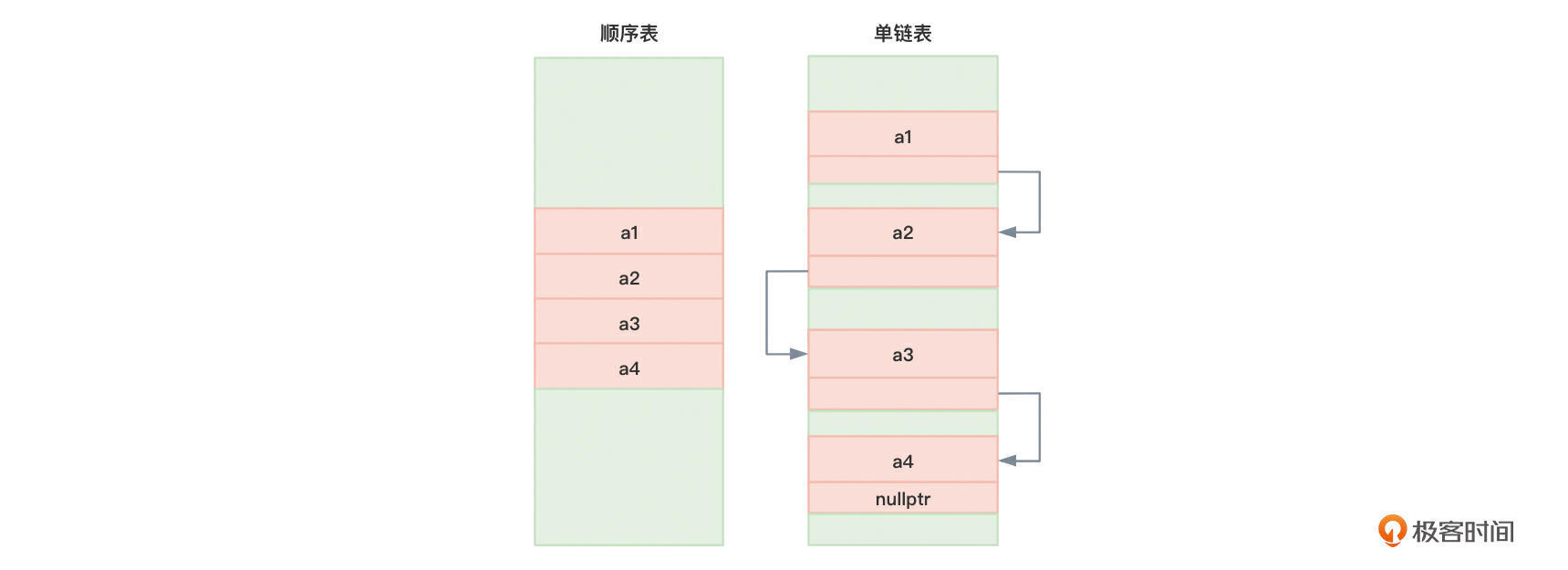
你可以看到，左侧顺序表中存储的元素在内存中紧密相连。其中，每个存储数据元素的内存空间被称为一个节点。

而右侧单链表中存储的元素在内存中并不需要紧密相连。在单链表中，每个节点不但用于存放一个数据元素（数据域），还要额外存放一个用于指向后继节点的指针也称后继指针（指针域），最后一个节点的指针域指向nullptr。

如果画得形象一点，单链表数据存储描述图应该是这样的：

在书写单链表相关代码时，有时为了更方便更统一的对链表进行操作，会在单链表的第一个节点之前再增设一个和其他节点类型相同的节点，称为头结点（也称哨兵节点）。

头结点的数据域可以不存储任何信息，也可以存储比如单链表长度等额外信息。头结点的指针域指向第一个节点。注意，头结点始终位于任何其他节点之前，就算我们需要向链表的首部插入节点，那插入的节点也要位于头结点之后。

带头结点的单链表画出数据存储描述图，就应该是这样的：

那不带头结点的单链表，和带头结点的单链表有什么不同呢？我们来对比一下。

**初始化时：**不带头结点的单链表（有时也称不带头链表）在初始化时不创建任何节点，而带头结点的单链表（有时也称带头链表）在初始化时要把头结点创建出来（可以把该头结点看成是第0个节点）。
**实际元素数据的位置：**带头结点的单链表中的头节点不存放实际元素数据。头节点之后的下一个节点才开始存放数据。
**代码操作：**不带头结点的单链表在编写基本操作代码（比如插入、删除等）时更繁琐，往往需要对第一个或者最后一个数据节点进行单独的处理。

在书写单链表的基本操作代码时，多数情况下，我们都会使用带头结点的代码实现方式，下面的讲解，我也会遵循这种书写方式。

单链表的类定义、初始化操作

我们还是和之前的讲解一样，先说类定义和初始化操作。从图2可以看到，单链表是由一个个的节点组成，所以，我们首先要定义出单个节点。

//单链表中每个节点的定义
template <typename T> //T代表数据元素的类型
struct Node
{
	T        data;    //数据域，存放数据元素
	Node<T>* next;  //指针域，指向下一个同类型（和本节点类型相同）节点
	};

接着定义单链表，书写单链表构造函数的代码。

//单链表的定义
template <typename T>
class LinkList
{
public:
	LinkList();      //构造函数
	~LinkList(){};     //析构函数
		
public:
	bool ListInsert(int i, const T& e);  //在第i个位置插入指定元素e
	bool ListDelete(int i);              //删除第i个位置的元素
		
	bool GetElem(int i, T& e);           //获得第i个位置的元素值
	int  LocateElem(const T& e);         //按元素值查找其在单链表中第一次出现的位置
		
	void DispList();                     //输出单链表中的所有元素
	int  ListLength();                   //获取单链表的长度
	bool Empty();                        //判断单链表是否为空
	void ReverseList();                  //翻转单链表
		
		
private:
	Node<T>* m_head; //头指针（指向链表第一个节点的指针，如果链表有头结点则指向头结点）
	int m_length;    //单链表当前长度（当前有几个元素），为编写程序更加方便和提高程序运行效率而引入，但不是必须引入
};
//通过构造函数对单链表进行初始化
template <typename T>
LinkList<T>::LinkList()
{		
	m_head = new Node<T>; //先创建一个头结点
	m_head->next = nullptr;
	m_length = 0;  //头结点不计入单链表的长度
}

在上面的LinkList类模板的构造函数中，通过new创建了一个头结点。在main主函数中，加入如下代码创建一个单链表对象。

1	LinkList<int> slinkobj;

到这里，单链表的类定义、初始化操作就完成了。

单链表元素插入操作

如果我们想在单链表的第i个位置插入指定的元素（也可以称为插入指定的节点），那么只需要找到单链表中的第i-1个节点并将新节点插入该节点之后即可。这里要注意，单链表中的位置编号从1开始，对于带头节点的单链表，我们不计算这个头节点的。

单看上面这段话有些绕，我们看一下把元素a5插入到单链表第2个位置前后对比图，会更好理解。

理解之后，我们就可以看下插入操作ListInsert的实现代码（带头结点）了。

//在第i个位置（位置编号从1开始）插入指定元素e
template <typename T>
bool LinkList<T>::ListInsert(int i, const T& e)
{
	//判断插入位置i是否合法，i的合法值应该是1到length+1之间
	if (i < 1 || i > (m_length + 1))
	{
		cout << "元素" << e << "插入的位置" << i << "不合法，合法的位置是1到" << m_length + 1 << "之间!" << endl;
		return false;
	}
		
	Node<T>* p_curr = m_head;
		
	//整个for循环用于找到第i-1个节点
	for (int j = 0; j < (i-1); ++j) //j从0开始，表示p_curr刚开始指向的是第0个节点（头结点）
	{
		p_curr = p_curr->next; //pcurr会找到当前要插入的位置，比如要在第2个位置插入，pcurr会指向第1个位置
	}
		
	①Node<T>* node = new Node<T>;
	②node->data = e;	
	③node->next = p_curr->next;//让新节点链上后续链表，因为pcurr->next指向后续的链表节点
	④p_curr->next = node;//让当前位置链上新节点，因为node指向新节点
		
	cout << "成功在位置为" << i << "处插入元素" << e << "!" << endl;
	m_length++;	        //实际表长+1
	return true;
	}

在上面的代码中，我们要重点关注前面增加了数字的代码行，其中的①、③、④行涉及到了新节点的创建以及修改新老节点的指向，那么这些行对应的节点指向示意图要怎么画呢？

你可以对照着上面这幅图加强理解，如果感觉有一定困难，那一定要直接通过跟踪调试代码的手段来学习，务必做到对每行代码都有透彻的领会。

说回来，在main主函数中，我们继续增加代码测试元素插入操作。

slinkobj.ListInsert(1, 12);
slinkobj.ListInsert(1, 24);
slinkobj.ListInsert(3, 48);
slinkobj.ListInsert(2, 100);

这样，新增代码的执行结果就会是：

同样，我们分析一下ListInsert的时间复杂度。这里只需要关注for循环的执行次数与问题规模n的关系，问题规模n在这里指的是单链表当前长度m_length。

如果将元素插入到单链表的开头（位置1），则for循环一次都不会执行，这是最好情况时间复杂度O(1)。
如果将元素插入到单链表的末尾，并且假设单链表中已经有其他元素（非空），则for循环会循环n-1次，这是最坏情况时间复杂度O(n)。
平均情况时间复杂度其实在顺序表中已经做过很详细的分析，这里很类似，平均情况时间复杂度为O(n)，时间开销主要源于插入位置的寻找。

另外，在实际的应用中，往往也会涉及到向某个已知节点之前插入一个新节点的情况。传统的做法是必须要利用头指针m_head从前向后找到该已知节点的前趋节点。参考前面图4，要将a5插入到a2之前必须要先从前向后找到a1节点，算法的平均情况时间复杂度为O(n)。

那有没有什么更好的方法呢？

将新节点a5插入到a2节点之后（a2节点是已知的无需查找）。
将a2和a5两个节点的数据域中的元素值互换。

如图6所示：

你看，最终也可以达到将a5插入到a2之前的效果，而且这样修改后的算法时间复杂度为O(1)。

如果有兴趣，你也可以自行实现该操作相关的算法代码，下面是算法命名和相关参数。

template<typename T>
bool LinkList<T>::InsertPriorNode(Node<T>* pcurr, const T& e)
{
	//在节点pcurr之前插入新节点，新节点数据域元素值为e，请自行添加相关代码......
	}

最后，如果需要频繁的向单链表的末尾插入新节点，从算法执行所耗费时间的角度去看，每次用for循环从前向后寻找插入位置的做法并不好。我们可以考虑引入一个表尾指针，这个指针在单链表为空时，会指向头结点，在单链表非空时，要注意始终保持其指向最后一个节点。这样，通过表尾指针在单链表的末尾插入新节点就会变得非常容易了。

单链表元素删除操作

关于删除操作，如果想删除单链表的第i个位置的元素，那只需要找到单链表中的第i-1个节点，并将其指针域指向第i+1个节点，同时释放第i个节点所占的内存，就可以了。

先来看删除操作ListDelete的实现代码（带头结点）。

//删除第i个位置的元素
template < typename T>
bool LinkList<T>::ListDelete(int i)
{
	if (m_length < 1)
	{
		cout << "当前单链表为空，不能删除任何数据!" << endl;
		return false;
	}
	if (i < 1 || i > m_length)
	{
		cout << "删除的位置" << i << "不合法，合法的位置是1到" << m_length << "之间!" << endl;
		return false;
	}
	
	Node<T>* p_curr = m_head;
		
	//整个for循环用于找到第i-1个节点
	for (int j = 0; j < (i - 1); ++j)//j从0开始，表示p_curr刚开始指向的是第0个节点（头结点）
	{
		p_curr = p_curr->next; //pcurr会找到当前要删除的位置所代表的节点的前一个节点的位置，比如要删除第2个位置的节点，pcurr会指向第1个位置(节点)
	}
	
	Node<T>* p_willdel = p_curr->next; //p_willdel指向待删除的节点
	p_curr->next = p_willdel->next; //第i-1个节点的next指针指向第i+1个节点
	cout << "成功删除位置为" << i << "的元素，该元素的值为" << p_willdel->data << "!" << endl;
	m_length--;       //实际表长-1
	delete p_willdel;
	return true;
	}

在main主函数中，我们需要继续增加代码测试元素删除操作。

1	slinkobj.ListDelete(4);

新增代码的执行结果就会是：

同样，我们分析一下ListDelete的时间复杂度。

如果删除单链表开头位置的节点，那么for循环一次都不会执行，这是最好情况时间复杂度O(1)。
如果删除单链表末尾位置的节点，并且假设单链表中已经有其他元素（非空），则for循环会循环n-1次，这是最坏情况时间复杂度O(n)。
平均情况时间复杂度在顺序表中也做过很详细的分析，这里很类似，平均情况时间复杂度为O(n)，时间开销主要源于删除位置的寻找。

在实际的应用中，往往我们也会涉及到删除某个指定节点的情况。传统的做法是必须要利用头指针m_head从前向后找到这个被删除节点的前趋节点。比如要将a2删除，就要先从前向后找到a1节点，算法的平均情况时间复杂度为O(n)。

想一想，怎么才能优化这个操作呢？

将a2后继节点a3中数据拷贝到a2节点的数据域中。
将a2节点的指针域指向a3的后继节点a4。
释放a3节点所占用的内存。

我们看一下这个流程的思路：

这样修改后的算法时间复杂度就是O(1)了。如果有兴趣，你也可以自行实现该操作相关的算法代码。下面是算法命名和相关参数。

template<class T>
bool LinkList<T>::DeleteNode(Node<T>* pdel)
{
	//删除pdel所指向的节点，请自行添加相关代码......
	}

但要注意，如果要删除的节点正好是单链表的最后一个节点，那就没法用上述快捷高效的方式来编写代码了（代码会报错）。我们还是必须用传统做法，利用头指针找到该将被删除节点的前趋节点，来删除某个指定节点。

单链表元素获取操作

在元素获取操作这里，通常分为两种情况：按位置获取和按元素值获取。

首先是按位置获取单链表中的元素值。

//获得第i个位置的元素值
template<class T>
bool LinkList<T>::GetElem(int i, T& e)
{
	if (m_length < 1)
	{
		cout << "当前单链表为空，不能获取任何数据!" << endl;
		return false;
	}
		
	if (i < 1 || i > m_length)
	{
		cout << "获取元素的位置" << i << "不合法，合法的位置是1到" << m_length << "之间!" << endl;
		return false;
	}
		
	Node<T>* p_curr = m_head;
	for (int j = 0; j < i; ++j)
	{
		p_curr = p_curr->next; 
	}
	e = p_curr->data;
	cout << "成功获取位置为" << i << "的元素，该元素的值为" << e << "!" << endl;
	return true;
	}

在main主函数中，我们继续增加代码测试按位置进行元素获取操作。

1 2	int eval = 0; slinkobj.GetElem(3, eval);//如果GetElem()返回true，则eval中保存着获取到的元素值

新增代码的执行结果就会是：

显然，按位置获取单链表元素操作的平均情况时间复杂度为O(n)。

另一种，按元素值查找其在单链表中第一次出现的位置，代码是下面这样的。

//按元素值查找其在单链表中第一次出现的位置
template<class T>
int LinkList<T>::LocateElem(const T& e)
{
	Node<T>* p_curr = m_head;
	for (int i = 1; i <= m_length; ++i)
	{
		if (p_curr->next->data == e)
		{
			cout << "值为" << e << "的元素在单链表中第一次出现的位置为" << i<< "!" << endl;
			return i; 
		}
		p_curr = p_curr->next;
	}
	cout << "值为" << e << "的元素在单链表中没有找到!" << endl;
	return -1;  //返回-1表示查找失败
	}

在main主函数中，我们继续增加代码测试按元素值查找其在单链表中第一次出现的位置。

1 2	int findvalue = 100; //在单链表中要找的元素值 slinkobj.LocateElem(findvalue);

新增代码的执行结果就会是：

按元素值查找其在单链表中第一次出现位置操作的平均情况时间复杂度，依旧为O(n)。

单链表元素的其他常用操作

目前为止，我们已经了解了单链表框架的搭建，元素的插入、删除、获取操作，除此之外，它还有其他一些常用操作，比如输出所有元素、获取单链表长度、翻转单链表等等。

我们分别看一下它们的具体实现。

输出单链表中的所有元素DispList

//输出单链表中的所有元素，时间复杂度为O(n)
template<class T>
void LinkList<T>::DispList()
{
	Node<T>* p = m_head->next;
	while (p != nullptr) //这里采用while循环或者for循环书写都可以
	{
		cout << p->data << " ";  //每个数据之间以空格分隔
		p = p->next;
	}
	cout << endl; //换行
	}

获取单链表的长度ListLength

//获取单链表的长度，时间复杂度为O(1)
template<class T>
int  LinkList<T>::ListLength()
{
	return m_length;
	}

判断单链表是否为空

//判断单链表是否为空，时间复杂度为O(1)
template<class T>
bool LinkList<T>::Empty()
{
	if (m_head->next == nullptr) //单链表为空（如果是不带头结点的单链表则用if(m_head == nullptr）来判断是否为空）
	{ 
		return true;
	}
	return false;
	}

翻转单链表ReverseList

所谓翻转单链表，就是把单链表中节点的排列顺序反过来。比如原来节点的排列顺序为a1、a2、a3、a4，那么翻转后节点的排列顺序就是a4、a3、a2、a1。

这里要注意的是，并不是针对节点数据域中的数据进行翻转，而是针对整个节点进行翻转（比如原来位于单链表尾部的节点经过翻转后排到了单链表的头部）。

我们先来考虑一下这种问题的解决思路。

把头节点和第一个节点分到一起作为第一部分。
把剩余的节点分成一部分。
每次从剩余的节点中的最前面拿出一个节点插入到第一部分单链表的首部。

图8展示了翻转单链表的步骤，先将头结点和a1分到一起作为第一部分，将a2、a3、a4分到一起作为第二部分，然后摘取第二部分的首部节点a2插到第一部分的a1之前，再摘取第二部分的首部节点a3插入到第一部分的a2之前……最终就可以实现整个单链表的翻转。

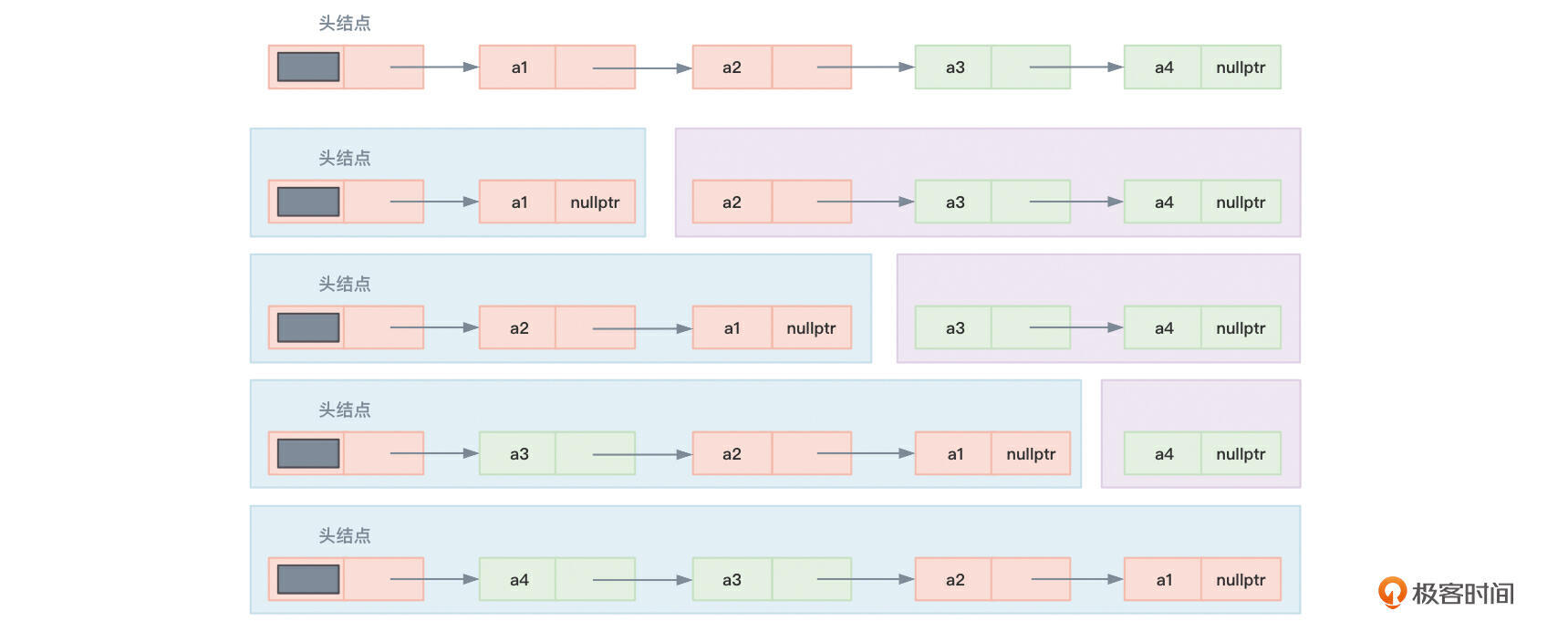
下面是具体的实现代码。

//翻转单链表，时间复杂度为O(n)
template <typename T>
void LinkList<T>::ReverseList()
{
	if (m_length <= 1)
	{
		//如果顺序表中没有元素或者只有一个元素，那么就不用做任何操作
		return;
	}
		
	//至少有两个节点才会走到这里
	Node<T>* pothersjd = m_head->next->next;   //指向从第二个节点开始的后续节点
	m_head->next->next = nullptr;              //第一个节点的指针域先置空
	
	Node<T>* ptmp;
	while (pothersjd != nullptr)
	{
		//比如a1、a2、a3、a4共4个节点，第一次执行该循环时的指向看下面代码中的注释
		ptmp = pothersjd;               //ptmp代表a2
		pothersjd = pothersjd->next;    //现在pothersjd指向a3
		
		ptmp->next = m_head->next;      //a2指向a1
		m_head->next = ptmp;		    //头结点指向a2 
	}
	}

在main主函数中，继续增加代码测试翻转单链表。

1
2
3

slinkobj.DispList();
slinkobj.ReverseList();
slinkobj.DispList();

新增代码的执行结果就会是：

单链表的释放操作

最后，我们说一下对单链表的释放工作，放到类模板LinkList的析构函数中是比较合适的。我们不但要释放单链表中带有数据的节点，也要释放头结点，目前LinkList析构函数的函数体是空的，我们注释掉它重写析构函数。

//通过析构函数对单链表进行资源释放，时间复杂度为O(n)
template <typename T>
LinkList<T>::~LinkList()
{
	Node<T>* pnode = m_head->next; 
	Node<T>* ptmp;
	while (pnode != nullptr) //该循环负责释放数据节点
	{
		ptmp = pnode;
		pnode = pnode->next;
		
		delete ptmp;
	}
	delete m_head;    //释放头结点
	m_head = nullptr; //非必须
	m_length = 0;     //非必须
	}

小结

这节课，我们首先给出了链表的定义和分类，然后开始讲述最基础的链表——单链表。因为不带头结点的单链表书写基本操作代码时更繁琐，所以引入了带头节点的单链表。

接着讲解了带头节点单链表的类定义及初始化操作、元素插入操作、元素删除操作、元素获取操作、释放操作等的实现代码。

总结下来，单链表有这样一些特点。

并不需要大片的连续存储空间来存放数据元素，扩容很方便。
插入和删除节点非常方便，平均情况时间复杂度为O(n)。当然，如果不考虑需要预先查找到插入和删除位置只单纯考虑插入和删除动作本身，那么时间复杂度仅为O(1)。不管怎么说，与数组相比，链表更适合插入、删除操作频繁的场景。
存放后继指针要额外消耗存储空间，体现了利用空间换时间来提高算法效率的编程思想。但对于内存紧张的硬件设备，就要考虑单链表是否适合使用了。
因为内存空间不连续，无法实现随机访问链表中的元素。要查找某个位置节点中的元素只能从链表的第一个节点开始沿着指针链逐个元素找下去，平均情况时间复杂度为O(n)。

因为单链表的操作代码相比于数组更加复杂，书写也更加容易出错，因此书写代码时除了要有清晰的逻辑思维之外，书写完毕后对代码进行测试也是非常重要和必要的——尤其是对边界情况的测试。在这里我也给出一些代码书写和测试的建议。

单链表是后面学习的其他链表的基础，因此应该通过多画图的方式理清代码逻辑，边看图边写自己认为正确的逻辑代码。
当链表为空的时候，测试代码能否正常工作。
当链表只有一个数据节点时，测试代码能否正常工作。
分别测试在处理链表中第一个和最后一个节点时代码能否正常工作。
发现程序执行异常并百思不得其解时，通过设置断点对代码进行调试，逐行跟踪并观察代码的执行情况就是必须的解决问题的手段。

归纳思考

参考带头节点的单链表，实现不带头节点的单链表，重点实现不带头节点单链表的元素插入操作代码。
你使用过C++标准模板库中的forward_list容器吗，你知道它是采用什么数据结构实现的吗？

欢迎你在留言区和我互动。如果觉得有所收获，也可以把课程分享给更多的朋友一起学习、进步。我们下一讲见！