你好，我是王健伟。

上节课我和你分享了用迪杰斯特拉（Dijkstra）算法求解最短路径。除此之外，还有一个求解最短路径的方法——佛洛依德（Floyd）算法。

那他们有什么不同吗？

如果说迪杰斯特拉算法比较适合一次性求某个顶点到其他各个顶点的最短路径信息，那么这节课所讲的佛洛依德算法往往比较适合求某个顶点到另外一个顶点的最短路径信息。

此外，迪杰斯特拉算法是不断计算从开始顶点到其他各个顶点的最短距离。而佛洛依德算法是通过从开始顶点到目标顶点之间不断增加新的顶点进行试探，看是否开始顶点和目标顶点之间的路径变短来求解最短路径的。

佛洛依德（Floyd）算法详解

这个算法是美国的一位计算机科学家罗伯特·弗洛伊德提出的，用于求解每一对顶点之间的最短路径。

这个算法实现的大致思路是什么呢？

那就是对任意一对顶点之间的最短路径的计算，都要进行|V|次试探。那么，每次试探都向图中加入一个新顶点，再去比较加入这个顶点之后这对要求解的顶点之间的最短路径是否变得更短，如果更短，则这条路径被采纳。以此类推，经过|V|次比较后，最后必然能够得到要求解的顶点之间的最短路径。

这里以图1所示的带权值有向图为例来讲解这个算法。图中同时展示了存储图中数据的邻接矩阵，为描述方便，我也标示出了每个顶点对应的下标。

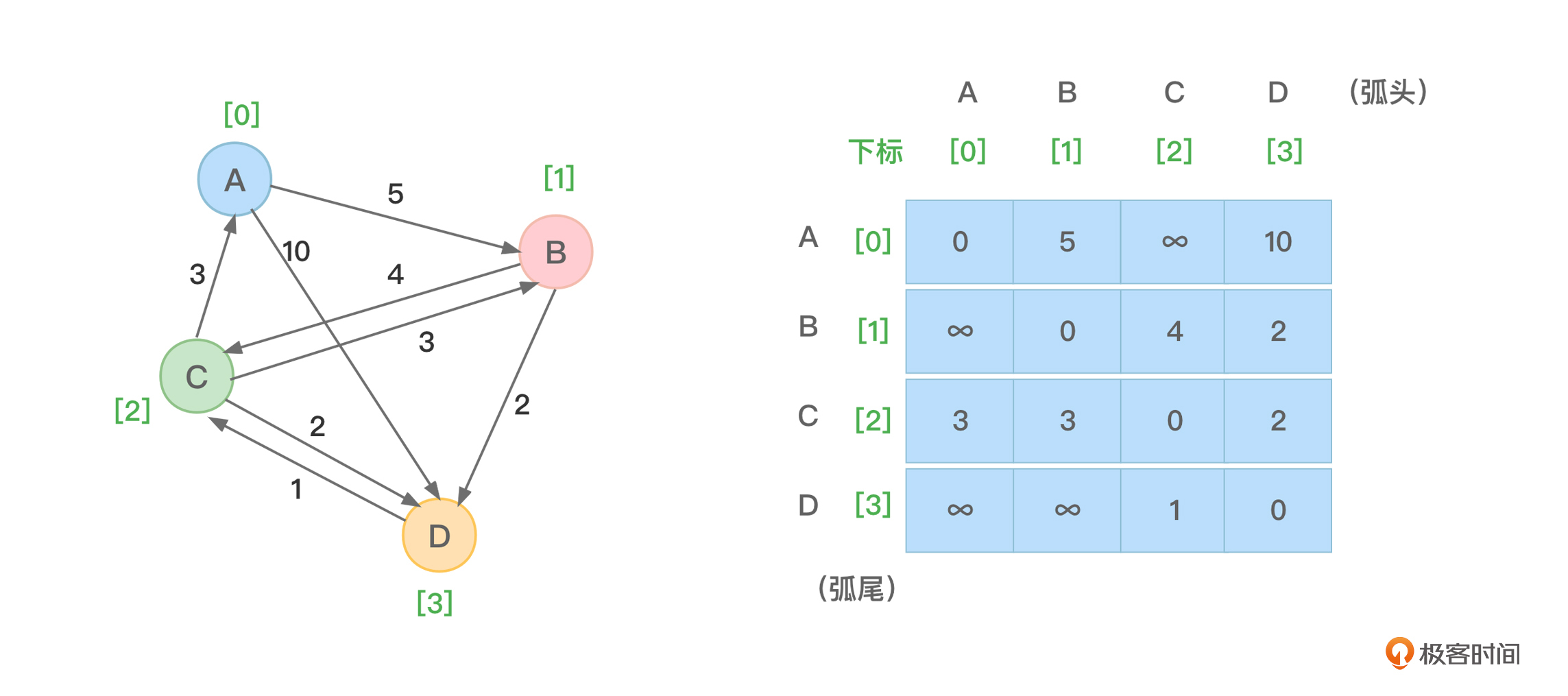
我们看一看弗洛伊德算法的编程思路。

步骤一

设置一个叫做dist的二维数组，用于存储图中任意两个顶点之间当前的最短路径长度信息，这个二维数组的起始内容就是该图相关的邻接矩阵信息，如下：

然后，设置一个叫做path的二维数组用于存储两个顶点所在最短路径上的中间点。这个二维数组中的每个元素开始都设置为-1，表示没有中间点：

弗洛伊德算法可以这样描述：依次向图中加入顶点v（v代表顶点的下标），每次加入顶点后都进行这样的操作：遍历上一个阶段得到的dist数组。dist数组的所有下标对（用[i][j]表示）中，如果i≠j并且v≠i,v≠j，则如果dist[i][j] > (dist[i][v]+ dist[v][j]),则将dist[i][j]的值更新为dist[i][v]+ dist[v][j]同时将path[i][j]值修改为v。这个描述非常重要，请你务必好好理解。

步骤二

开始计算，先把图中第一个顶点A（下标为0，即v=0）加入到有向图中，此时要考察加入顶点A之后，任意两个顶点之间的距离会不会因为顶点A的加入变得比原来更短。对于图1，根据弗洛伊德算法描述中的前提条件i≠j并且v≠i,v≠j，dist数组中满足这个条件的成员只有如下6个：

接着开始分析判断：
dist[1][2] = 4；而dist[1][0]+ dist[0][2] = ∞，忽略（后续忽略的将不再写出）。

……

经过比较，发现没有任何两个顶点之间的距离会因为顶点A的加入而变得更短，所以本次dist和path数据都不需要更新。

步骤三

好，我们继续把图中第二个顶点B（下标为1，即v=1）加入到有向图中，考察加入顶点B之后，任意两个顶点之间的距离会不会因为顶点B的加入而变得比原来更短。根据弗洛伊德算法描述中的前提条件i≠j并且v≠i,v≠j，dist数组中满足这个条件的成员只有如下6个：

开始分析判断：

更新dist数组，更新后的内容如下：

path数组相应的位置也要进行修改，修改为顶点B的下标值，更新后的内容如下：

步骤四

我们继续把图中第三个顶点C（下标为2，即v=2）加入到有向图中，考察加入顶点C之后，任意两个顶点之间的距离会不会因为顶点C的加入而变得比原来更短。根据弗洛伊德算法描述中的前提条件i≠j并且v≠i,v≠j，dist数组中满足这个条件的成员只有如下6个：

接着开始分析判断：

更新dist数组，更新后的内容如下：

path数组相应的位置也要进行修改，修改为顶点C的下标值，更新后的内容如下：

然后，把图中第四个顶点D（下标为3，即v=3）加入到有向图中，考察加入顶点D之后，任意两个顶点之间的距离会不会因为顶点D的加入而变得比原来更短。根据弗洛伊德算法描述中的前提条件i≠j并且v≠i,v≠j，dist数组中满足这个条件的成员只有如下6个：

开始分析判断：

更新dist数组，更新后的内容如下：

path数组相应的位置也要进行修改，修改为顶点C的下标值，更新后的内容如下：

步骤五

在将图中所有顶点都加入到有向图中并完成最短路径判断操作后，弗洛伊德算法结束，这个时候，顶点之间的最短路径大小以及路径信息就保存在了dist数组和path数组中。

这里我们尝试找顶点B（下标为1）到顶点A（下标为0）的最短路径。

  • 因为dist[1][0] = 6，所以顶点B到顶点A的最短路径权值是6。
  • 查询path[1][0] = 3，这意味着中间点[3]（顶点D）。即意味着[1]（顶点B）要先到顶点[3]（顶点D）……，最后才会到[0]（顶点A）。
  • 这相当于[3]插入到了[1]和[0]之间，即[1][3][0]。针对这三个下标数据，要分别查询，也就是要查询path[1][3]和path[3][0]。
  • 查询path[1][3] = -1，这说明[1]（顶点B）和[3]（顶点D）之间没有中间点，是直接连接的。
  • 查询path[3][0] = 2，这意味着中间点[2]（顶点C）。即意味着[3]（顶点D）要先到顶点[2]（顶点C）……，最后才会到[0]（顶点A）。目前的情形就是：[1][3][2][0]。那么就要查询path[3][2]和path[2][0]。
  • 查询path[3][2] = -1，这说明[3]（顶点D）和[2]（顶点C）之间没有中间点，是直接连接的。
  • 查询path[2][0] = -1，这说明[2]（顶点C）和[0]（顶点A）之间没有中间点，是直接连接的。
  • 所以最短边路径就找到了，下标是[1][3][2][0]，对应的顶点是B、D、C、A。这意味着从顶点B到顶点A的最短路径是B、D、C、A。

佛洛依德（Floyd）算法实现源码

根据我们上面逐步分析的思路，现在，我们可以尝试书写弗洛伊德（Floyd）算法的代码了。

下面是弗洛伊德（Floyd）算法的相关源码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
//弗洛伊德（Floyd）算法求任意两个顶点之间的最短路径
bool ShortestPath_Floyd(const T& tmpv1, const T& tmpv2) //tmpv1：开始顶点，tmpv2：结束顶点
{
	int idx1 = GetVertexIdx(tmpv1);
	if (idx1 == -1) //开始顶点不存在
		return false;
	
	int idx2 = GetVertexIdx(tmpv2);
	if (idx2 == -1) //结束顶点不存在
		return false;
	
	if (idx1 == idx2)
	{
		cout <<"开始顶点和结束顶点不可以相同！"<< endl;
		return false;
	}
	
	int** pdist = new int* [m_numVertices];
	int** ppath = new int* [m_numVertices];
	for (int i = 0; i < m_numVertices; ++i)
	{
		pdist[i] = new int[m_numVertices];
		ppath[i] = new int[m_numVertices];
	} //end for
	
	//二维数组初始化
	for (int i = 0; i < m_numVertices; ++i)
	{
		for (int j = 0; j < m_numVertices; ++j)
		{
			pdist[i][j] = pm_Edges[i][j];
			ppath[i][j] = -1;
		}//end j
	} //end i
	
	//用三重循环实现弗洛伊德（Floyd）算法
	for (int v = 0; v < m_numVertices; ++v)//依次把各个顶点放入图中，顶点下标是v
	{
		for (int i = 0; i < m_numVertices; ++i)
		{
			for (int j = 0; j < m_numVertices; ++j)
			{
				if (i == j || v == i || v == j)
					continue;
				
				if (pdist[i][v] == INT_MAX_MY || pdist[v][j] == INT_MAX_MY) //因为这两个数字将做加法操作，所以每个值都必须不能是INT_MAX_MY
				{
					continue;
				}
				else if (pdist[i][j] > (pdist[i][v] + pdist[v][j]))
				{
					pdist[i][j] = pdist[i][v] + pdist[v][j];
					ppath[i][j] = v;
				}
			} //end j
		} //end i
	} //end v
		
	//显示两个顶点之间最短路径信息
	if (pdist[idx1][idx2] == INT_MAX_MY )
	{
		cout <<"从顶点"<< pm_VecticesList[idx1] <<"到顶点"<< pm_VecticesList[idx2] <<"之间没有路径"<< endl;
	}
	else
	{
		cout <<"从顶点"<< pm_VecticesList[idx1] <<"到顶点"<< pm_VecticesList[idx2] <<"最短路径长度("<< pdist[idx1][idx2] <<")，最短路径：";
		Disp_FloydPath(ppath,idx1,idx2); //采用一个递归函数来显示最短路径信息
	}
	
	//释放内存
	for (int i = 0; i < m_numVertices; ++i)
	{
		delete[] pdist[i];
		delete[] ppath[i];
	} //end for
	delete[] pdist;
	delete[] ppath;
	return true;
}
	
//显示弗洛伊德（Floyd）算法找到的两点之间最小路径（递归函数）
void Disp_FloydPath(int** ppath,int u,int v)
{
	if (ppath[u][v] == -1)
	{
		cout <<"<"<< pm_VecticesList[u] <<"→"<< pm_VecticesList[v] <<">";
	}
	else
	{
		int middle = ppath[u][v];
		Disp_FloydPath(ppath, u, middle);
		Disp_FloydPath(ppath, middle, v);
	}
}

在main主函数中，增加如下测试代码：

1
gm.ShortestPath_Floyd('A', 'F');

新增代码执行结果如下：

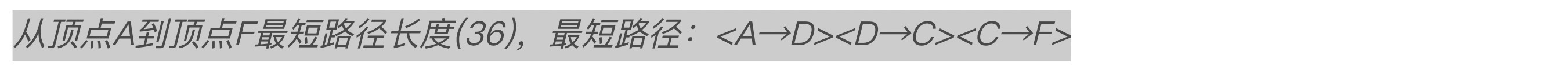
从代码中可以看到，显示两个顶点之间的路径信息采用的是一个递归函数Disp_FloydPath。因为代码中用到了三重循环，所以弗洛伊德（Floyd）算法的时间复杂度为O($|V|^{3}$)。

小结

这节课，我带你学习了利用佛洛依德算法求解顶点之间的最短路径。我详细描述了这个算法的思路和实现细节，对后续理清代码书写的思路非常有帮助。我们不得不佩服算法大师聪明的头脑和缜密的逻辑思维。

佛洛依德算法通过多次试探，每次试探都向图中加入一个新顶点并比较加入该顶点后要求得的两个顶点之间距离是否变得更短来决定新选择的路径是否被采纳。算法思路很简单，当然这不意味着编写程序就简单。

事实上，程序的编写还是具有一定复杂性的，注意，我们需要通过引入两个二维数组分别为dist和path来存储图中任意两点之间当前最短路径长度以及存储两个顶点所在最短路径上的中间点。

归纳思考

  1. 请你想一想，日常生活中的哪些问题可以采用弗洛伊德算法来解决呢？
  2. 请尝试总结佛洛依德算法与迪杰斯特拉算法的区别。

欢迎你在留言区分享自己的思考。如果觉得有所收获，也可以把课程分享给更多的朋友一起交流进步。我们下一讲见！

Share