52、计数排序：不通过比较也可以进行排序

你好，我是王健伟。

前面我们学习了许多种类的排序，这次我带你学习一种不同思想的排序种类——桶思想排序。桶排序有什么不同吗？如果说前面的排序主要是通过关键字的比较和记录的移动，而桶思想的排序往往并不需要进行关键字的比较。

桶一般指生活里的一种容器，在这里其实是一个比较形象的说法，一般指排序过程中用到的诸如计数数组、辅助队列等用于临时容纳数据的地方。

这节课我将带你学习一下桶思想排序中的计数排序算法，计数排序算法有一定的编写技巧，我们将首先实现一个非稳定的计数排序算法，通过进一步改进代码来实现稳定的计数排序算法，让我们开始这次的学习旅程吧。

非稳定的计数排序算法的实现

计数排序是通过计数而不是比较来进行排序的。算法比较简单，适合于待排序记录数量多但排序关键字的范围比较小的整数数字排序情形。

比如某大型公司有10万名员工，按照员工年龄进行排序这种情形就非常适合计数排序。再比如有1000万人参加高考，满分750分，根据自己的分数来计算自己的名次，这也明显是一个排序问题，用计数排序也很合适。

计数排序的思想是创建一个新数组用于计数，数组的大小取决于要排序的关键字最大值是多少。比如大型公司的这个案例，排序关键字是年龄，而年龄一般不会超过90岁，所以这个新数组的大小为90即可。

假设有一些员工的年龄是{35,22,53,33,35,29,35,55,60,33,21,29,22,52,37,46,40,29}。

可以看到，有一些员工的年龄是重复的。现在，引入一个计数数组（也可以称为桶），起名叫做ArrayCount，开始时该数组中所有元素的初值都设置为0。

将员工的年龄作为数组元素下标并开始计数——遇到年龄相同员工的就把对应的数组元素值加1，然后开始计数。计数的结果应该是这样的。

ArrayCount[35]=3;    //这表示35岁的员工有3位
ArrayCount[22]=2;    //这表示22岁的员工有2位
ArrayCount[53]=1;    //这表示53岁的员工有1位
ArrayCount[33]=2;    
ArrayCount[29]=3;  
ArrayCount[55]=1;  
ArrayCount[60]=1;  
ArrayCount[21]=1;  
ArrayCount[52]=1;  
ArrayCount[37]=1;  
ArrayCount[46]=1;  
ArrayCount[40]=1;

有了这个计数数组之后，从下标0开始遍历该数组，根据计数数组当前的情形，忽略掉计数为0的数组元素，则最先遍历到的肯定是ArrayCount[21]，发现其计数为1，则输出一个21，继续遍历肯定会遍历到ArrayCount[22]，发现其计数为2，则输出两个22——22、22，再继续遍历肯定会遍历到ArrayCount[29]，发现其计数为3，则输出三个29——29、29、29……这样自然就可以按照从小到大的顺序把关键字排好序了。

你可以看下具体的实现代码。

//计数排序
template<typename T>
void CountSort(T myarray[], int length, T maxvalue) //maxvalue：要排序的关键字最大值
{
	T* pArrayCount = new T[maxvalue];		
	for (int i = 0; i < maxvalue; ++i) //清0
	{
		pArrayCount[i] = 0;
	}
	
	for (int i = 0; i < length; ++i)
	{
		pArrayCount[myarray[i]] ++;
	}
	
	int idx = 0; //下标索引
	for (int i = 0; i < maxvalue; ++i)
	{
		if (pArrayCount[i] == 0) //没计数的自然忽略掉
			continue;
		
		//有计数
		for (int j = 0; j < pArrayCount[i]; ++j)
		{
			myarray[idx] = i;
			idx++;
		}
	}
	delete[] pArrayCount;
	return;
}

在main主函数中，可以用多组数据进行测试，这里我依旧用10个元素的数组做测试。

int arr[] = { 16,1,45,23,99,2,18,67,42,10 };
int length = sizeof(arr) / sizeof(arr[0]);   //数组中元素个数
CountSort(arr, length,99 + 1);//对数组元素进行计数排序，注意最大元素值+1，以给计数数组留出空间
cout <<"计数排序结果为：";
for (int i = 0; i < length; ++i)
{
cout << arr[i] <<"";
}
cout << endl; //换行

代码的执行结果如下：

如果遇到要排序的数字是负数呢？也不要紧，我们总可以确定要排序的整数数字的最大值和最小值从而确定出计数数组定义多大合适。当然，在根据计数数组来输出排序结果时，计数数组下标为0的元素代表的应该是待排序关键字中的最小值，而不再是0本身。比如，对-10到10之间的元素排序，定义的计数数组大小应该是21（最大值-最小值+1）。而计数数组下标为0的元素代表的应该是-10。

计数排序算法效率分析

计数排序算法的时间复杂度方面，因为要扫描待排序的n个元素，还需要用到辅助的计数数组来进行计数统计工作，这里用k代表计数数组的大小，所以计数排序算法的时间复杂度为O(n+k)，当然因为k值取值范围比较小，可能远远小于n值，所以也可以把计数排序算法的时间复杂度看成是O(n)。因为用到了计数数组，所以，空间复杂度是O(k)。

前面曾经强调过，计数排序的适用场合是：

待排序记录数量多。
排序关键字的范围比较小。
整数数字排序。

此时用计数排序可能比其他排序算法要快得多。但如果不满足这样的场合，则要慎用这样的排序，以免造成排序效率过差。

计数排序算法稳定性问题以及算法空间复杂度的改变

对于计数排序算法的稳定性问题，目前的代码实现是很难认定算法是稳定的，或者说现在这个代码是不稳定的。必须对代码进行一些小改动才能让其稳定。

在讲解改动代码之前，我准备举一个非常简单的范例以作为对这些代码的解释。有20个数字，这些数字最大值不超过5，最小值不小于0，需要用计数排序进行排序，这些数字是：1，3，5，1，0，5，4，1，2，3，4，3，2，5，4，4，4，4，2，0。

按照前面实现的计数排序代码，引入计数数组ArrayCountS，大小为6就足够了。然后开始计数。计数的结果应该是：

ArrayCountS[0] = 2;  
ArrayCountS[1] = 3;
ArrayCountS[2] = 3;
ArrayCountS[3] = 3;
ArrayCountS[4] = 6;
ArrayCountS[5] = 3;

如图1所示。

现在，如果对图1的计数数组接着执行如下代码，看一看该计数数组的内容会有什么变化？

for (int i = 1; i < maxvalue; ++i)//maxvalue=6，代表计数数组大小
{
	ArrayCountS [i] = ArrayCountS [i] + ArrayCountS [i - 1];
}

代码中可以清晰地看到，后一个计数数组元素的值变成了当前值+前一个数组元素的值，执行完上述代码后，ArrayCountS数组的值变成了如下图2所示，也有人把此时的ArrayCountS数组称为累加数组或累计数组。

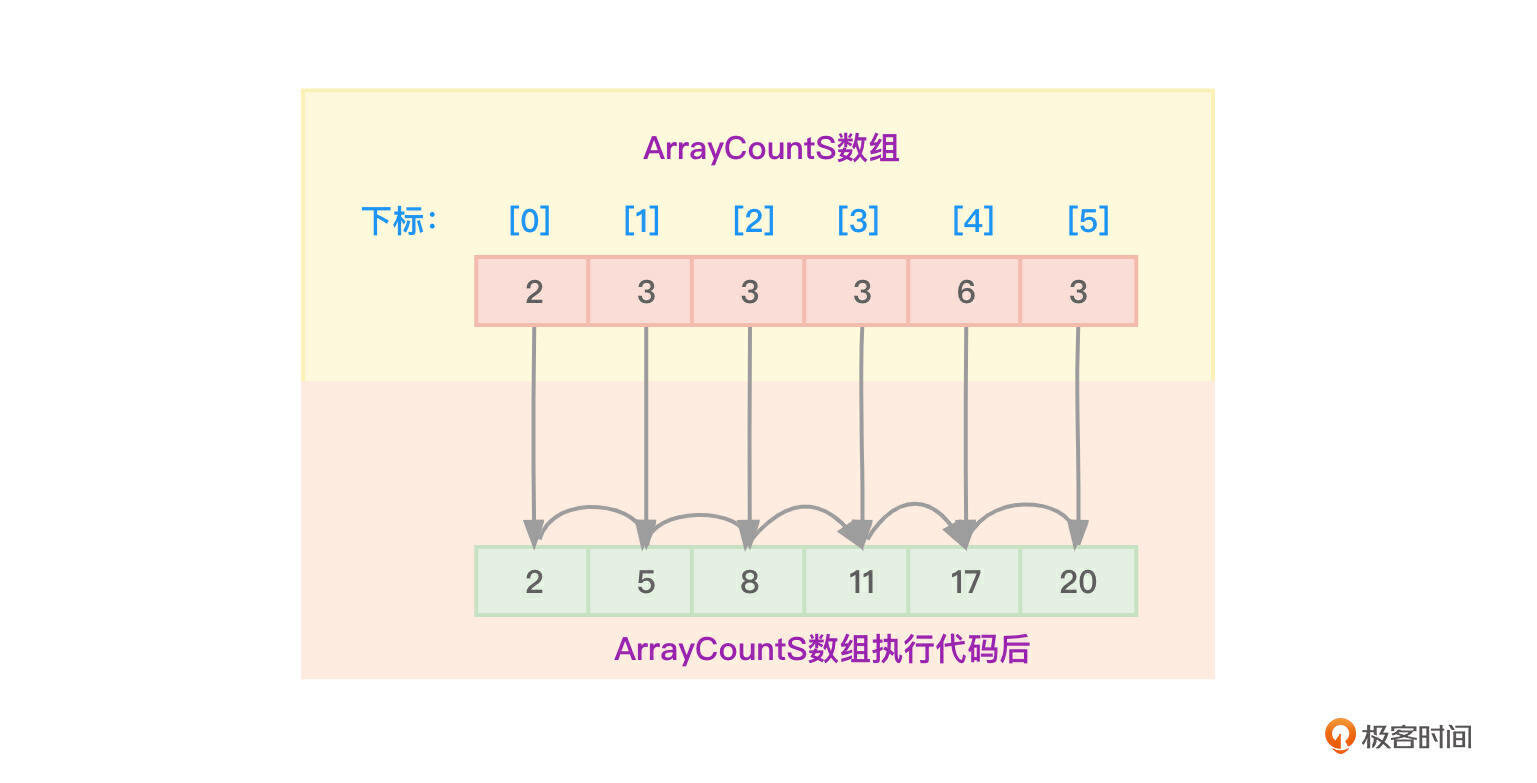
图2可以看到，执行上述代码后，ArrayCountS数组的值从原来的2、3、3、3、6、3变成了2、5、8、11、17、20。这些改变后的数字意味着什么？其实很简单，这些数字代表的是一个位置信息，严格来讲代表的是“最后位置”信息。

目前待排序的数字一共有20个，所以需要创建一个和元素数组同样大小的辅助数组（大小为20）。看一下ArrayCountS数组中每个数值的含义。

20：对应的计数数组下标为5，这代表如果遇到待排序的那个数字是5，就把5放到辅助数组的第20个位置（下标为19），然后20这个数字减1变成19，代表着下次遇到待排序的数字5会把这个5放到辅助数组的第19个位置。
17：对应的计数数组下标为4，这代表如果遇到待排序的那个数字是4，就把4放到辅助数组的第17个位置（下标为16），然后17这个数字减1变成16。
11：对应的计数数组下标为3，这代表如果遇到待排序的那个数字是3，就把3放到辅助数组的第11个位置（下标为10），然后11这个数字减1变成10。
8、5、2：和前面的20、17、11都是同样的意思。

现在开始倒序遍历要排序的数组：{1,3,5,1,0,5,4,1,2,3,4,3,2,5,4,4,4,4,2,0}。

第一个遍历到的数字是0，ArrayCountS[0]当前值为2，所以，把这个数字0放在辅助数组下标为2-1=1的位置。同时ArrayCountS[0]当前值减少1，变成了1。
第二个遍历到的数字是2，ArrayCountS[2]当前值为8，所以，把这个数字2放在辅助数组下标为8-1=7的位置，同时ArrayCountS[2]当前值为8减少1，变成了7。
依此类推。

根据上面的描述，可以很容易地把剩余的实现代码写出来。下面是完整的计数排序算法稳定版。

//计数排序（稳定）（从小到大）
template<typename T>
void CountSort(T myarray[], int length, T maxvalue) //maxvalue：要排序的关键字最大值
{
	T* pArrayCount = new T[maxvalue];
	for (int i = 0; i < maxvalue; ++i) //清0
	{
		pArrayCount[i] = 0;
	}
	
	for (int i = 0; i < length; ++i)
	{
		pArrayCount[myarray[i]] ++;
	}
	
	for (int i = 1; i < maxvalue; ++i)
	{
		pArrayCount[i] = pArrayCount[i] + pArrayCount[i - 1];
	} //end for
	
	//创建辅助数组
	T* pFZArray = new T[length]; 

	//倒序遍历要排序的数组
	for (int i = length - 1; i >= 0; --i)
	{
		int idx = pArrayCount[myarray[i]] - 1;
		pFZArray[idx] = myarray[i];
		pArrayCount[myarray[i]]--;
	} //end for 
		
	//把排好序的内容写回来
	for (int i = 0; i < length; ++i)
	{
		myarray[i] = pFZArray[i];
	}
	//释放内存
	delete[] pFZArray;
	delete[] pArrayCount;
	return;
}

上述的计数排序算法就是稳定的了。从代码中可以看到，因为创建了一个和源数组大小相同的辅助数组以保存必要的排序结果信息，所以此时空间复杂度就不再是O(k)而是O(n+k)。

另外，你可以想一想，如何对数据进行倒序（从大到小）排列？那就要在计数数组ArrayCountS变成累加数组ArrayCountS的过程中做文章了，把如下代码段：

for (int i = 1; i < maxvalue; ++i)
{
	pArrayCount[i] = pArrayCount[i] + pArrayCount[i - 1];
}

修改为：

for (int i = maxvalue - 1; i > 0; --i)
{
	pArrayCount[i - 1] = pArrayCount[i - 1] + pArrayCount[i];
}

像上面这样修改后，计数数组ArrayCountS就变成了如下这样的累加数组ArrayCountS，如图3所示。

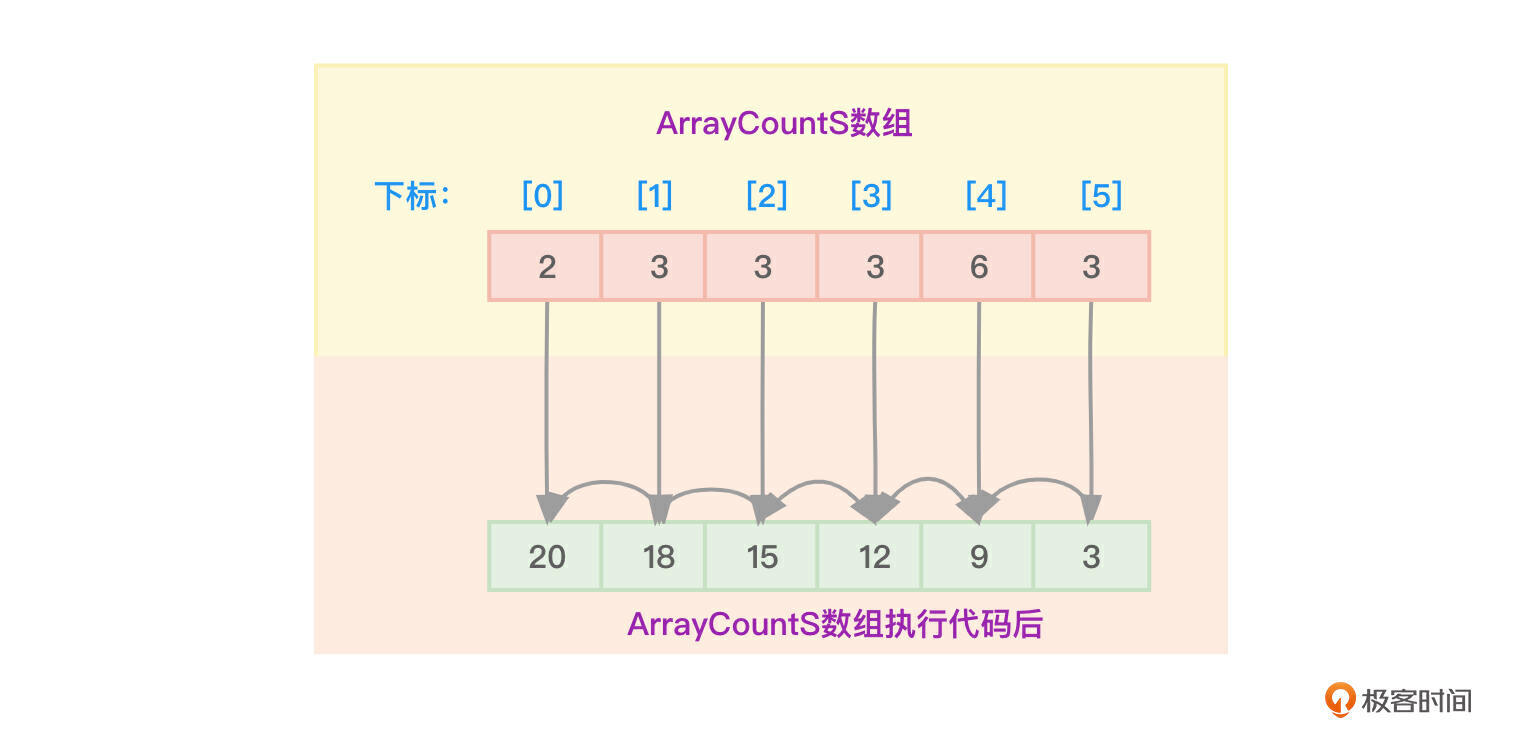
现在开始倒序遍历要排序的数组：1,3,5,1,0,5,4,1,2,3,4,3,2,5,4,4,4,4,2,0。

第一个遍历到的数字是0，ArrayCountS[0]当前值为20，所以，把这个数字0放在辅助数组下标为20-1=19的位置。同时ArrayCountS[0]当前值减少1，变成了19。
第二个遍历到的数字是2，ArrayCountS[2]当前值为15，所以，把这个数字2放在辅助数组下标为15-1=14的位置，同时ArrayCountS[2]当前值为15减少1，变成了14。
依此类推。

输入一下结果，发现数据已经从大到小排序了，并且算法是稳定的。

小结

这节课我们引入了一个新的排序分类——桶思想排序，我为你详细讲解了该类排序中的计数排序算法。

计数排序是通过计数而非比较来进行排序的。算法比较简单，适合于待排序记录数量多，但排序关键字的范围比较小的整数数字排序情形。我详细为你讲解了计数排序的思想、步骤以及实现代码，并带你详细分析了算法的执行效率。

此外，针对算法的稳定性问题我也进行了详细地说明，并通过对代码的改进来实现稳定的计数排序算法，你要注意的是在实现稳定算法的过程中，算法的空间复杂度会发生变化，从O(k)变成O(n+k)。

思考题

在这节课的最后，我也给你留了2道复习思考题。

仔细想一想什么时候适合使用计数排序算法？
什么情况下计数排序算法会出现性能方面的问题？

欢迎你在留言区和我互动。如果觉得有所收获，也可以把课程分享给更多的同学一起学习，我们下节课见！